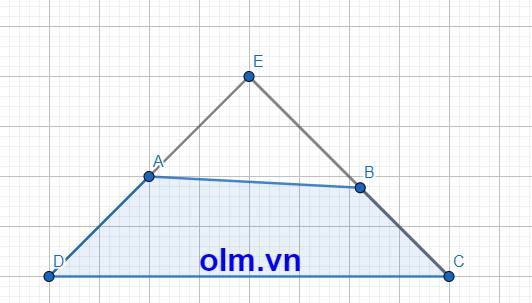
Kéo dài DA và CB lần lượt về phía A và B cắt nhau tại E
Xét tam giác DCE có \(\widehat{DEC}\) = 1800 - (\(\widehat{EDC}\) + \(\widehat{ECD}\)) = 1800- 900 = 900
⇒\(\Delta\)DEC vuông tại E
Xét \(\Delta\)AEB Theo pytago ta có: AE2 + BE2 = AB2
Tương tự ta có: DE2 + CE2 = DC2
Cộng vế với vế ta có: AE2 + BE2 + DE2 + CE2 = AB2+DC2
AE2 + CE2+BE2+DE2 = AB2+DC2 (1)
Xét \(\Delta\)AEC theo pytago ta có: AE2+ CE2 = AC2
Tương tự ta có: BE2 + DE2 = BD2
Cộng vế với vế ta có: AE2 + CE2 + BE2+ DE2 = AC2 + BD2 (2)
Từ (1) và (2) ta có: AC2 + BD2 = AB2 + DC2(đpcm)









