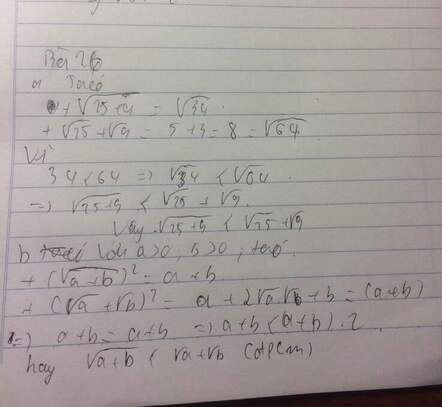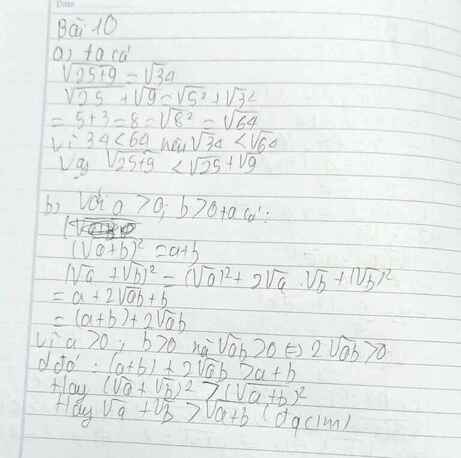Question

Bài 26 (trang 16 SGK Toán 9 Tập 1)

a) So sánh $\sqrt{25+9}$ và $\sqrt{25}+\sqrt{9}$ ;

b) Với $a>0$ và $b>0$, chứng minh $\sqrt{a+b}<\sqrt{a}+\sqrt{b}$.

Answer 1

a) Ta có: 

+)√25+9=√34+)25+9=34.

+)√25+√9=√52+√32=5+3+)25+9=52+32=5+3

=8=√82=√64=8=82=64.

Vì 34<6434<64 nên √34<√6434<64

Vậy √25+9<√25+√925+9<25+9

b) Với a>0,b>0a>0,b>0, ta có

+)(√a+b)2=a+b+)(a+b)2=a+b.

+)(√a+√b)2=(√a)2+2√a.√b+(√b)2+)(a+b)2=(a)2+2a.b+(b)2

 =a+2√ab+b=a+2ab+b

 =(a+b)+2√ab=(a+b)+2ab. 

Vì a>0, b>0a>0, b>0 nên √ab>0⇔2√ab>0ab>0⇔2ab>0

⇔(a+b)+2√ab>a+b⇔(a+b)+2ab>a+b

⇔(√a+√b)2>(√a+b)2⇔(a+b)2>(a+b)2

⇔√a+√b>√a+b⇔a+b>a+b (đpcm)

Answer 2

a, Ta có : \(\sqrt{25+9}=\sqrt{34}\)

\(\sqrt{25}+\sqrt{9}=5+3=8=\sqrt{64}\)

mà 34 < 64 hay \(\sqrt{25+9}< \sqrt{25}+\sqrt{9}\)

b, \(\sqrt{a+b}< \sqrt{a}+\sqrt{b}\)

bình phương 2 vế ta được : \(a+b< a+2\sqrt{ab}+b\)

\(\Leftrightarrow2\sqrt{ab}>0\)vì \(a;b>0\)nên đẳng thức này luôn đúng )

Vậy ta có đpcm 

Answer 3

a) \(\sqrt{25+9}=\sqrt{34}\)

\(\sqrt{25}+\sqrt{9}=5+3=8=\sqrt{64}\)

=> \(\sqrt{25+9}< \sqrt{25}+\sqrt{9}\)

b) Vì a,b > 0, bình phương hai vế ta có :

a + b < a + 2√ab + b

<=> -2√ab < 0 <=> 2√ab > 0 ( đúng vì a,b > 0 )

=> đpcm

Answer 4

a) Ta có: 

+) $\sqrt{25+9}=\sqrt{34}$.

+) $\sqrt{25}+\sqrt{9}=\sqrt{5^2}+\sqrt{3^2}$

$=5+3=8=\sqrt{8^2}=\sqrt{64}$.

Vì $34<64$ nên $\sqrt{34}<\sqrt{64}$

Vậy $\sqrt{25+9}<\sqrt{25}+\sqrt{9}$.

b) Với $a>0,b>0$ ta có:

+) $(\sqrt{a+b}{)}^2=a+b$.

+) $(\sqrt{a}+\sqrt{b}{)}^2=(\sqrt{a}{)}^2+2\sqrt{a}.\sqrt{b}+(\sqrt{b}{)}^2$

 $=a+2\sqrt{ab}+b$

 $=(a+b)+2\sqrt{ab}$. 

Vì $a>0,b>0$ nên $\sqrt{ab}>0$ $\iff$ $2\sqrt{ab}>0$

Do đó: $(a+b)+2\sqrt{ab}>a+b$

Hay $(\sqrt{a}+\sqrt{b}{)}^2>(\sqrt{a+b}{)}^2$

Hay $\sqrt{a}+\sqrt{b}>\sqrt{a+b}$ (đpcm)

Answer 5

a ) căn 25 + 9 < căn 25 + căn 9

b) Với $a>0,b>0$ ta có:

+) (\sqrt{a+b})^2=a+b(+)2=a+b.

+) (\sqrt{a}+\sqrt{b})^2=(\sqrt{a})^2+2\sqrt{a}.\sqrt{b}+(\sqrt{b})^2(a​+b​)2=(a​)2+2a​.b​+(b​)2

 =a+2\sqrt{ab}+b=a+2ab​+b

 =(a+b)+2\sqrt{ab}=(a+b)+2ab​. 

Vì $a>0,b>0$ nên \sqrt{ab}>0ab​>0 $\iff$ 2\sqrt{ab}>02ab​>0

Do đó: (a+b)+2\sqrt{ab}>a+b(a+b)+2ab​>a+b

Hay (\sqrt{a}+\sqrt{b})^2>(\sqrt{a+b})^2(a​+b​)2>(+)2

Hay \sqrt{a}+\sqrt{b}>\sqrt{a+b}a​+b​>+ (đpcm)

Answer 6

a) Ta có: 

$+)\sqrt{25+9}=\sqrt{34}$.

$+)\sqrt{25}+\sqrt{9}=\sqrt{5^2}+\sqrt{3^2}=5+3$

$=8=\sqrt{8^2}=\sqrt{64}$.

Vì $34<64$ nên $\sqrt{34}<\sqrt{64}$

Vậy $\sqrt{25+9}<\sqrt{25}+\sqrt{9}$

b) Với $a>0,b>0$, ta có

$+\left)\right(\sqrt{a+b}{)}^2=a+b$.

$+\left)\right(\sqrt{a}+\sqrt{b}{)}^2=(\sqrt{a}{)}^2+2\sqrt{a}.\sqrt{b}+(\sqrt{b}{)}^2$

 $=a+2\sqrt{ab}+b$

 $=(a+b)+2\sqrt{ab}$. 

Vì $a>0,b>0$ nên $\sqrt{ab}>0\iff 2\sqrt{ab}>0$

$\iff (a+b)+2\sqrt{ab}>a+b$

$\iff (\sqrt{a}+\sqrt{b}{)}^2>(\sqrt{a+b}{)}^2$

$\iff \sqrt{a}+\sqrt{b}>\sqrt{a+b}$ (đpcm

Answer 7

a) Ta có: 

+) $\sqrt{25+9}=\sqrt{34}$.

+) $\sqrt{25}+\sqrt{9}=\sqrt{5^2}+\sqrt{3^2}$

$=5+3=8=\sqrt{8^2}=\sqrt{64}$.

Vì $34<64$ nên $\sqrt{34}<\sqrt{64}$

Vậy $\sqrt{25+9}<\sqrt{25}+\sqrt{9}$.

b) Với $a>0,b>0$ ta có:

+) $(\sqrt{a+b}{)}^2=a+b$.

+) $(\sqrt{a}+\sqrt{b}{)}^2=(\sqrt{a}{)}^2+2\sqrt{a}.\sqrt{b}+(\sqrt{b}{)}^2$

 $=a+2\sqrt{ab}+b$

 $=(a+b)+2\sqrt{ab}$. 

Vì $a>0,b>0$ nên $\sqrt{ab}>0$ $\iff$ $2\sqrt{ab}>0$

Do đó: $(a+b)+2\sqrt{ab}>a+b$

Hay $(\sqrt{a}+\sqrt{b}{)}^2>(\sqrt{a+b}{)}^2$

Hay $\sqrt{a}+\sqrt{b}>\sqrt{a+b}$ (đpcm)

Answer 8

a) Ta có: 

+) $\sqrt{25+9}=\sqrt{34}$.

+) $\sqrt{25}+\sqrt{9}=\sqrt{5^2}+\sqrt{3^2}$

$=5+3=8=\sqrt{8^2}=\sqrt{64}$.

Vì $34<64$ nên $\sqrt{34}<\sqrt{64}$

Vậy $\sqrt{25+9}<\sqrt{25}+\sqrt{9}$.

b) Với $a>0,b>0$ ta có:

+) $(\sqrt{a+b}{)}^2=a+b$.

+) $(\sqrt{a}+\sqrt{b}{)}^2=(\sqrt{a}{)}^2+2\sqrt{a}.\sqrt{b}+(\sqrt{b}{)}^2$

 $=a+2\sqrt{ab}+b$

 $=(a+b)+2\sqrt{ab}$. 

Vì $a>0,b>0$ nên $\sqrt{ab}>0$ $\iff$ $2\sqrt{ab}>0$

Do đó: $(a+b)+2\sqrt{ab}>a+b$

Hay $(\sqrt{a}+\sqrt{b}{)}^2>(\sqrt{a+b}{)}^2$

Hay $\sqrt{a}+\sqrt{b}>\sqrt{a+b}$ (đpcm)

Answer 9

Answer 10

a) \(\sqrt{25+9}=\sqrt{34};\sqrt{25}+\sqrt{9}=5+3=8;\sqrt{34}< \sqrt{64}=8\Rightarrow\sqrt{25+9}< \sqrt{25}+\sqrt{9}\)

b)   \(\sqrt{a+b}^2=a+b;\left(\sqrt{a}+\sqrt{b}\right)^2=a+2\sqrt{ab}+b;a+b< a+b+2\sqrt{ab}\)

Answer 11

Answer 12

Answer 13

Answer 14

Answer 15

Answer 16

a) \(\sqrt{25+9}\) = \(\sqrt{34}\) ≈ 5.83
    \(\sqrt{25}\) + \(\sqrt{9}\) = 5 + 3 = 8
   ⇒ \(\sqrt{25}\) + \(\sqrt{9}\) > \(\sqrt{25+9}\)
b) Suy ngược ⇔ \(\sqrt{a+b}\) < \(\sqrt{a}\) + \(\sqrt{b}\)
                       ⇔ \(\sqrt{a+b}^2\) < \(\left(\sqrt{a}+\sqrt{b}\right)^2\)
                       ⇔  a + b    <   a + 2\(\sqrt{ab}\) + b
                       ⇔           0 < 2\(\sqrt{ab}\) ( a>0;b>0)

Answer 17

Answer 18

a) 

\sqrt{25+9}<\sqrt{25}+\sqrt{9}25+9​<25​+9

b)  \sqrt{a}+\sqrt{b}>\sqrt{a+b}a​+b​>a+b​

Answer 19

Answer 20

Answer 21

 

Answer 22

Answer 23

a) Ta có: 
\(\sqrt{25+9}=\sqrt{34}\)
\(\sqrt{25}+\sqrt{9}=\sqrt{\left(5\right)^2}+\sqrt{\left(3\right)^2}=\left|5\right|+\left|3\right|=5+3=8=\sqrt{64}\)
Vì \(34< 64\Rightarrow\sqrt{34}< \sqrt{64}\)
\(\Rightarrow\sqrt{25+9}< \sqrt{25}+\sqrt{9}\)
Vậy \(\sqrt{25+9}< \sqrt{25}+\sqrt{9}\)

b)Ta có:
\(\left(\sqrt{a+b}\right)^2=a+b\left(a>0;b>0\right)\)
\(\left(\sqrt{a}+\sqrt{b}\right)^2=a+2\sqrt{ab}+b=\left(a+b\right)+2\sqrt{ab}\)
Vì \(a>0;b>0\Rightarrow\sqrt{ab}>0\)
\(\Leftrightarrow2\sqrt{ab>0}\)
\(\Leftrightarrow\left(a+b\right)+2\sqrt{ab}=a+b\)
\(\Leftrightarrow\left(\sqrt{a}+\sqrt{b}\right)^2>\left(\sqrt{a+b}\right)^2\)
\(\Leftrightarrow\sqrt{a+b}< \sqrt{a}+\sqrt{b}\left(đpcm\right)\)

Answer 24

a) Ta có: 

+) $\sqrt{25+9}=\sqrt{34}$.

+) $\sqrt{25}+\sqrt{9}=\sqrt{5^2}+\sqrt{3^2}$

$=5+3=8=\sqrt{8^2}=\sqrt{64}$.

Vì $34<64$ nên $\sqrt{34}<\sqrt{64}$

Vậy $\sqrt{25+9}<\sqrt{25}+\sqrt{9}$.

b) Với $a>0,b>0$ ta có:

+) $(\sqrt{a+b}{)}^2=a+b$.

+) $(\sqrt{a}+\sqrt{b}{)}^2=(\sqrt{a}{)}^2+2\sqrt{a}.\sqrt{b}+(\sqrt{b}{)}^2$

 $=a+2\sqrt{ab}+b$

 $=(a+b)+2\sqrt{ab}$. 

Vì $a>0,b>0$ nên $\sqrt{ab}>0$ $\iff$ $2\sqrt{ab}>0$

Do đó: $(a+b)+2\sqrt{ab}>a+b$

Hay $(\sqrt{a}+\sqrt{b}{)}^2>(\sqrt{a+b}{)}^2$

Hay $\sqrt{a}+\sqrt{b}>\sqrt{a+b}$ (đpcm)

Answer 25

a) Ta có: 

+) \sqrt{25+9}=\sqrt{34}25+9​=34​.

+) \sqrt{25}+\sqrt{9}=\sqrt{5^2}+\sqrt{3^2}25​+9​=52​+32​

=5+3=8=\sqrt{8^2}=\sqrt{64}=5+3=8=82​=64​.

Vì $34<64$ nên \sqrt{34}<\sqrt{64}34​<64​

Vậy \sqrt{25+9}<\sqrt{25}+\sqrt{9}25+9​<25​+9​.

b) Với $a>0,b>0$ ta có:

+) (\sqrt{a+b})^2=a+b(a+b​)2=a+b.

+) (\sqrt{a}+\sqrt{b})^2=(\sqrt{a})^2+2\sqrt{a}.\sqrt{b}+(\sqrt{b})^2(a​+b​)2=(a​)2+2a​.b​+(b​)2

 =a+2\sqrt{ab}+b=a+2ab​+b

 =(a+b)+2\sqrt{ab}=(a+b)+2ab​. 

Vì $a>0,b>0$ nên \sqrt{ab}>0ab​>0 $\iff$ 2\sqrt{ab}>02ab​>0

Do đó: (a+b)+2\sqrt{ab}>a+b(a+b)+2ab​>a+b

Hay (\sqrt{a}+\sqrt{b})^2>(\sqrt{a+b})^2(a​+b​)2>(a+b​)2

Hay \sqrt{a}+\sqrt{b}>\sqrt{a+b}a​+b​>a+b​ (đpcm)

Answer 26

Answer 27

a) Ta có: 

+) $\sqrt{25+9}=\sqrt{34}$.

+) $\sqrt{25}+\sqrt{9}=\sqrt{5^2}+\sqrt{3^2}$

$=5+3=8=\sqrt{8^2}=\sqrt{64}$.

Vì $34<64$ nên $\sqrt{34}<\sqrt{64}$

Vậy $\sqrt{25+9}<\sqrt{25}+\sqrt{9}$.

b) Với $a>0,b>0$ ta có:

+) $(\sqrt{a+b}{)}^2=a+b$.

+) $(\sqrt{a}+\sqrt{b}{)}^2=(\sqrt{a}{)}^2+2\sqrt{a}.\sqrt{b}+(\sqrt{b}{)}^2$

 $=a+2\sqrt{ab}+b$

 $=(a+b)+2\sqrt{ab}$. 

Vì $a>0,b>0$ nên $\sqrt{ab}>0$ $\iff$ $2\sqrt{ab}>0$

Do đó: $(a+b)+2\sqrt{ab}>a+b$

Hay $(\sqrt{a}+\sqrt{b}{)}^2>(\sqrt{a+b}{)}^2$

Hay $\sqrt{a}+\sqrt{b}>\sqrt{a+b}$ (đpcm)

Answer 28

a) Ta có: 

+) \sqrt{25+9}=\sqrt{34}25+9​=34​.

+) \sqrt{25}+\sqrt{9}=\sqrt{5^2}+\sqrt{3^2}25​+9​=52​+32​

=5+3=8=\sqrt{8^2}=\sqrt{64}=5+3=8=82​=64​.

Vì $34<64$ nên \sqrt{34}<\sqrt{64}34​<64​

Vậy \sqrt{25+9}<\sqrt{25}+\sqrt{9}25+9​<25​+9​.

b) Với $a>0,b>0$ ta có:

+) (\sqrt{a+b})^2=a+b(a+b​)2=a+b.

+) (\sqrt{a}+\sqrt{b})^2=(\sqrt{a})^2+2\sqrt{a}.\sqrt{b}+(\sqrt{b})^2(a​+b​)2=(a​)2+2a​.b​+(b​)2

 =a+2\sqrt{ab}+b=a+2ab​+b

 =(a+b)+2\sqrt{ab}=(a+b)+2ab​. 

Vì $a>0,b>0$ nên \sqrt{ab}>0ab​>0 $\iff$ 2\sqrt{ab}>02ab​>0

Do đó: (a+b)+2\sqrt{ab}>a+b(a+b)+2ab​>a+b

Hay (\sqrt{a}+\sqrt{b})^2>(\sqrt{a+b})^2(a​+b​)2>(a+b​)2

Hay \sqrt{a}+\sqrt{b}>\sqrt{a+b}a​+b​>a+b​ (đpcm)

Answer 29

a) Ta có: 

+) √25+9=√34.

22

2=√64.

Vì 34<64 nên √34<√64

Vậy √25+9<√25+√9.

b) Với a>0,b>0 ta có:

2=a+b.

222

 =a+2√ab+b

 =(a+b)+2√ab. 

Vì a>0,b>0 nên √ab>0 ⇔ 2√ab>0

Do đó: (a+b)+2√ab>a+b

22

Hay √a+√b>√a+b (đpcm)

 

Answer 30