Question

 bài 20 mình đang cần gấp 😭😭

Answer 1

20a/

$(x+1)(y-3)=15$

Với $x,y$ nguyên thì $x+1, y-3$ cũng là số nguyên. Mà tích $(x+1)(y-3)=15$ nên ta có bảng sau:

Answer 2

20b/

$5x(y-1)+y=5$

$5x(y-1)+(y-1)=4$

$(y-1)(5x+1)=4$

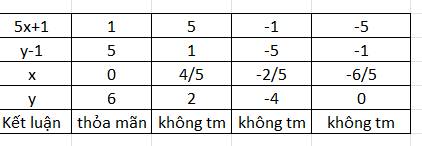
Do $x,y$ nguyên nên $5x+1, y-1$ cũng nguyên. Mà $(5x+1)(y-1)=4$ nên ta có bảng sau:

Answer 3

20c/

Ta thấy: 

$(x+1)^2\geq 0; (y-1)^2\geq 0$ với mọi $x,y$

$\Rightarrow (x+1)^2+(y-1)^2\geq 0$ với mọi $x,y$

Do đó để $(x+1)^2+(y-1)^2\leq 0$ như đề yêu cầu thì $(x+1)^2=(y-1)^2=0$

$\Leftrightarrow x=-1; y=1$