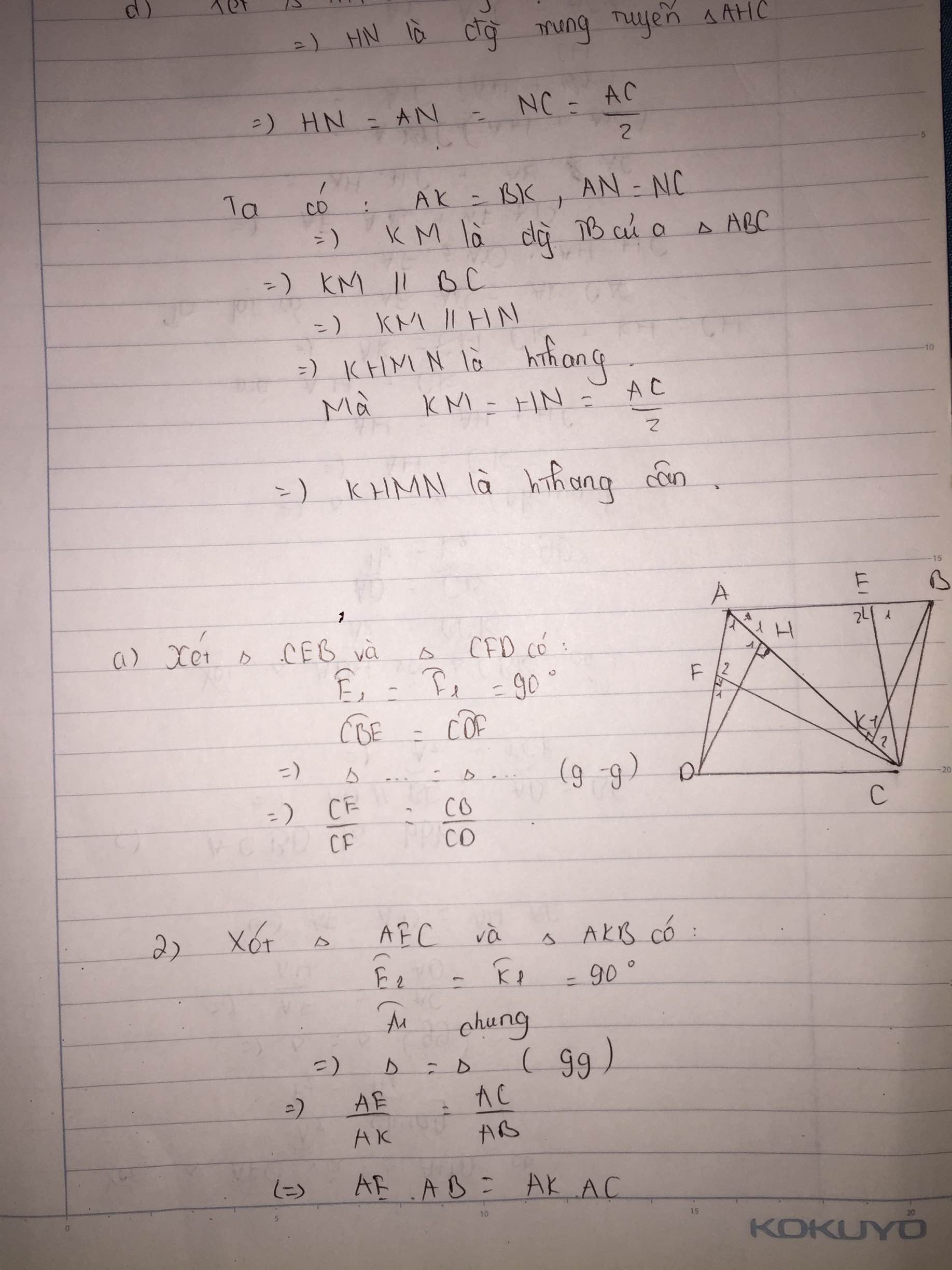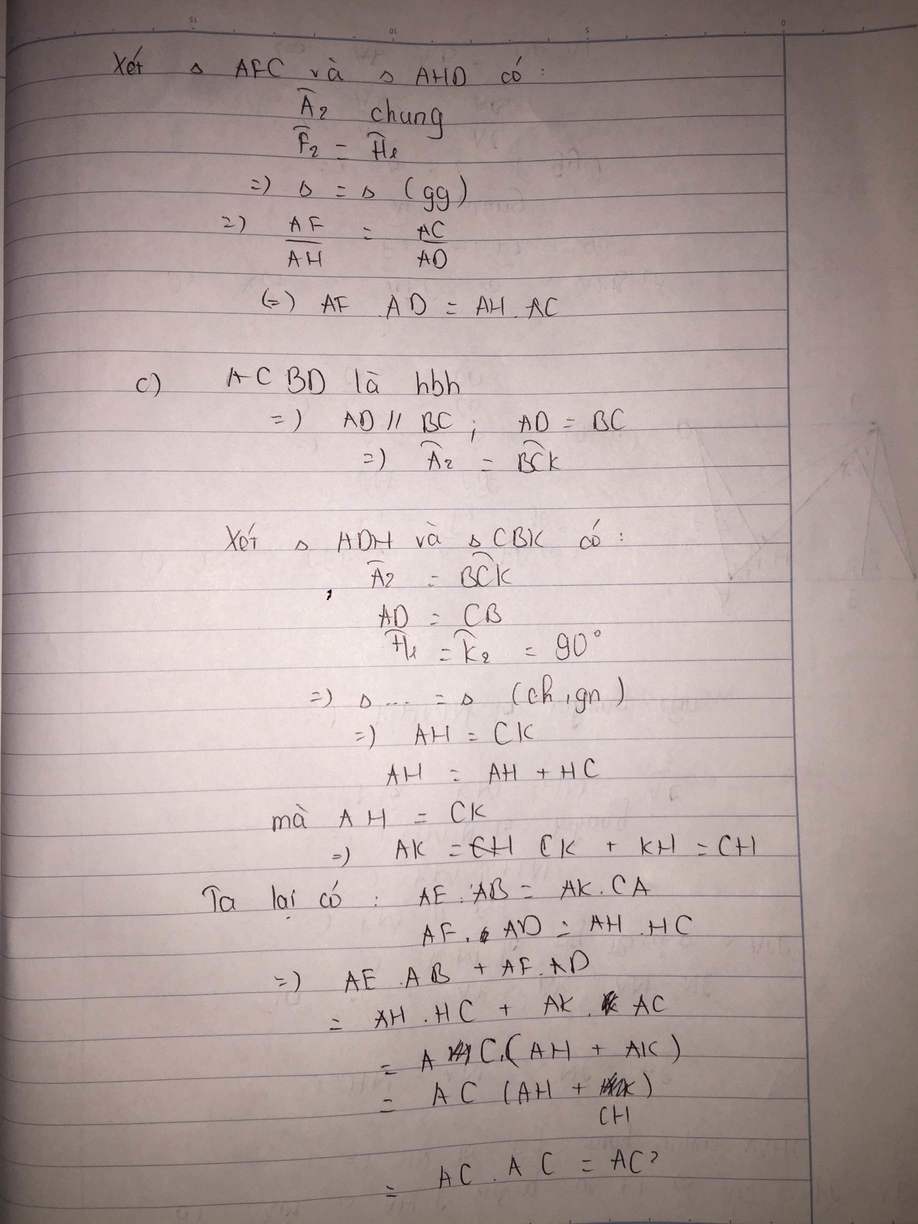Các câu hỏi tương tự
Cho AC là đường chéo lớn của hình bình hành ABCD. Từ C kẻ CE vuông góc với AB, kẻ CF vuông góc với AD (E,F thuộc AB và AD). Chứng minh rằng: AB*AE+AD*AF=AC2
Cho hình bình hành ABCD ( AB > AD) Từ C kẻ CE và CF vuông góc với đường thẳng AB , AD ( E thuộc AB , F thuộc AD) . Chứng minh
AB.AE + AD.AF = AC^2
Cho hình bình hành ABCD (góc BAD nhỏ hơn 90 độ) . Từ B kẻ Bm vuông góc AC(M thuộc AC), Từ C kẻ CE vuông góc AB, kẻ CF vuông góc AD (E thuộc AB, F thuộc AD) . chứng minh rằng
a)tam giác AMB đồng dạng tam giác AEC
b) \(\frac{CE}{CF}=\frac{CB}{CD}\)
c) \(\widehat{CAF}=\widehat{CEF}\)
Bài 1: Cho hình bình hành ABCD có đường chéo lớn AC,tia Dx cắt SC, AB, BC lần lượt tại I, M, N. Vẽ CE vuông góc với AB, CF vuông góc với AD, BG vuông góc với AC. Gọi K là điểm đối xứng với D qua I. Chứng minh rằnga) IM. IN ID2b)dfrac{text{KM}}{text{KN }} dfrac{text{DM}}{text{DN}}c) AB. AE + AD. AF AC2(VẼ CẢ HÌNH)
Đọc tiếp
Bài 1: Cho hình bình hành ABCD có đường chéo lớn AC,tia Dx cắt SC, AB, BC lần lượt tại I, M, N. Vẽ CE vuông góc với AB, CF vuông góc với AD, BG vuông góc với AC. Gọi K là điểm đối xứng với D qua I. Chứng minh rằng
a) IM. IN = ID2
b)\(\dfrac{\text{KM}}{\text{KN }}\)= \(\dfrac{\text{DM}}{\text{DN}}\)
c) AB. AE + AD. AF = AC2
(VẼ CẢ HÌNH)
Cho hình bình hành ABCD (AC > BD). Vẽ CE vuông góc với AB và CF vuông góc với AD. Chứng minh AB.AE + AD.AF = AC^2
Cho hình bình hành ABCD (AB > AD). Từ C vẽ CE, CF lần lượt vuông góc với các đường thẳng AB, AD (E thuộc AB, F thuộc AD). Chứng minh rằng AB.AE + AD.AF = AC2.
Cho hình bình hành ABCD có Ac là đường chéo lớn. Từ C kẻ CE vuông góc với đường thẳng Ab (E\(\in\)AB) và kẻ CF vuông góc với đường thẳng AD (F\(\in\)AD). Chứng minh \(AB.AE+AD.AF=AC^2\)
Cho hình bình hành ABCD , AC là đường chéo lớn . Kẻ CE vuông góc với AB tại E , CF vuông góc với AD tại F , BI vuông góc với AC tại I a, chứng minh tam giác AIB đồng dạng với tam giác AEC b, chưng minh tam giác AIE đồng dạng với tam giác ABC c, chứng minh AB . AE + AF . CB AC2d, tia BI cắt đường thẳng CD tại Q và căt cạnh AD tại K . chứng minh BI2 IK . IQ
Đọc tiếp
Cho hình bình hành ABCD , AC là đường chéo lớn . Kẻ CE vuông góc với AB tại E , CF vuông góc với AD tại F , BI vuông góc với AC tại I
a, chứng minh tam giác AIB đồng dạng với tam giác AEC
b, chưng minh tam giác AIE đồng dạng với tam giác ABC
c, chứng minh AB . AE + AF . CB = AC2
d, tia BI cắt đường thẳng CD tại Q và căt cạnh AD tại K . chứng minh BI2 = IK . IQ
Cho hình bình hành ABCD , AC là đường chéo lớn . Kẻ CE vuông góc với AB tại E , CF vuông góc với AD tại F , BI vuông góc với AC tại I a, chứng minh tam giác AIB đồng dạng với tam giác AEC b, chưng minh tam giác AIE đồng dạng với tam giác ABC c, chứng minh AB . AE + AF . CB AC2d, tia BI cắt đường thẳng CD tại Q và căt cạnh AD tại K . chứng minh BI2 IK . IQ
Đọc tiếp
Cho hình bình hành ABCD , AC là đường chéo lớn . Kẻ CE vuông góc với AB tại E , CF vuông góc với AD tại F , BI vuông góc với AC tại I
a, chứng minh tam giác AIB đồng dạng với tam giác AEC
b, chưng minh tam giác AIE đồng dạng với tam giác ABC
c, chứng minh AB . AE + AF . CB = AC2
d, tia BI cắt đường thẳng CD tại Q và căt cạnh AD tại K . chứng minh BI2 = IK . IQ