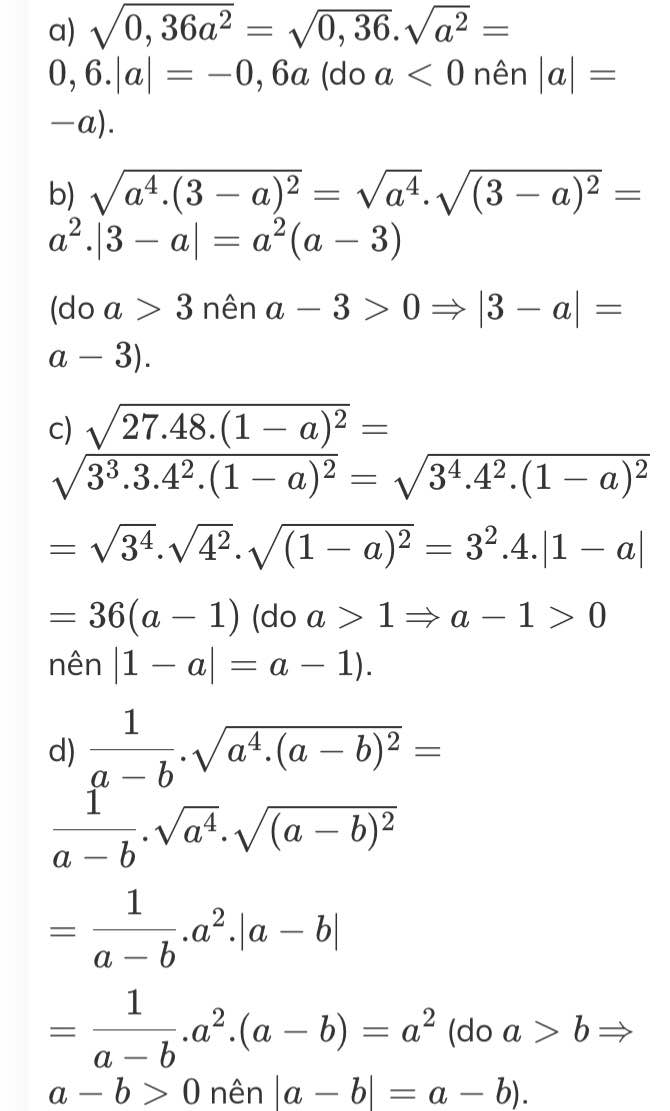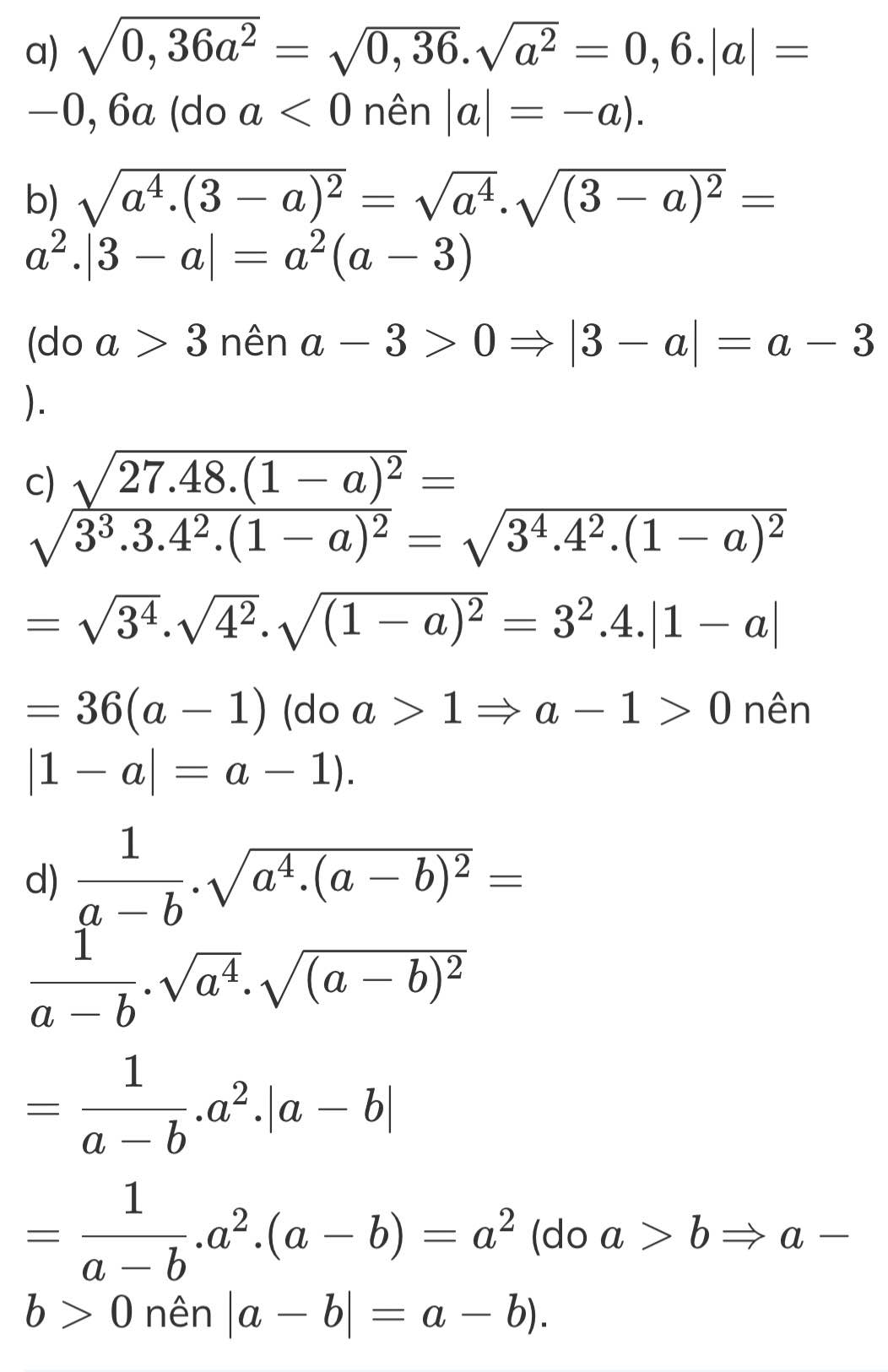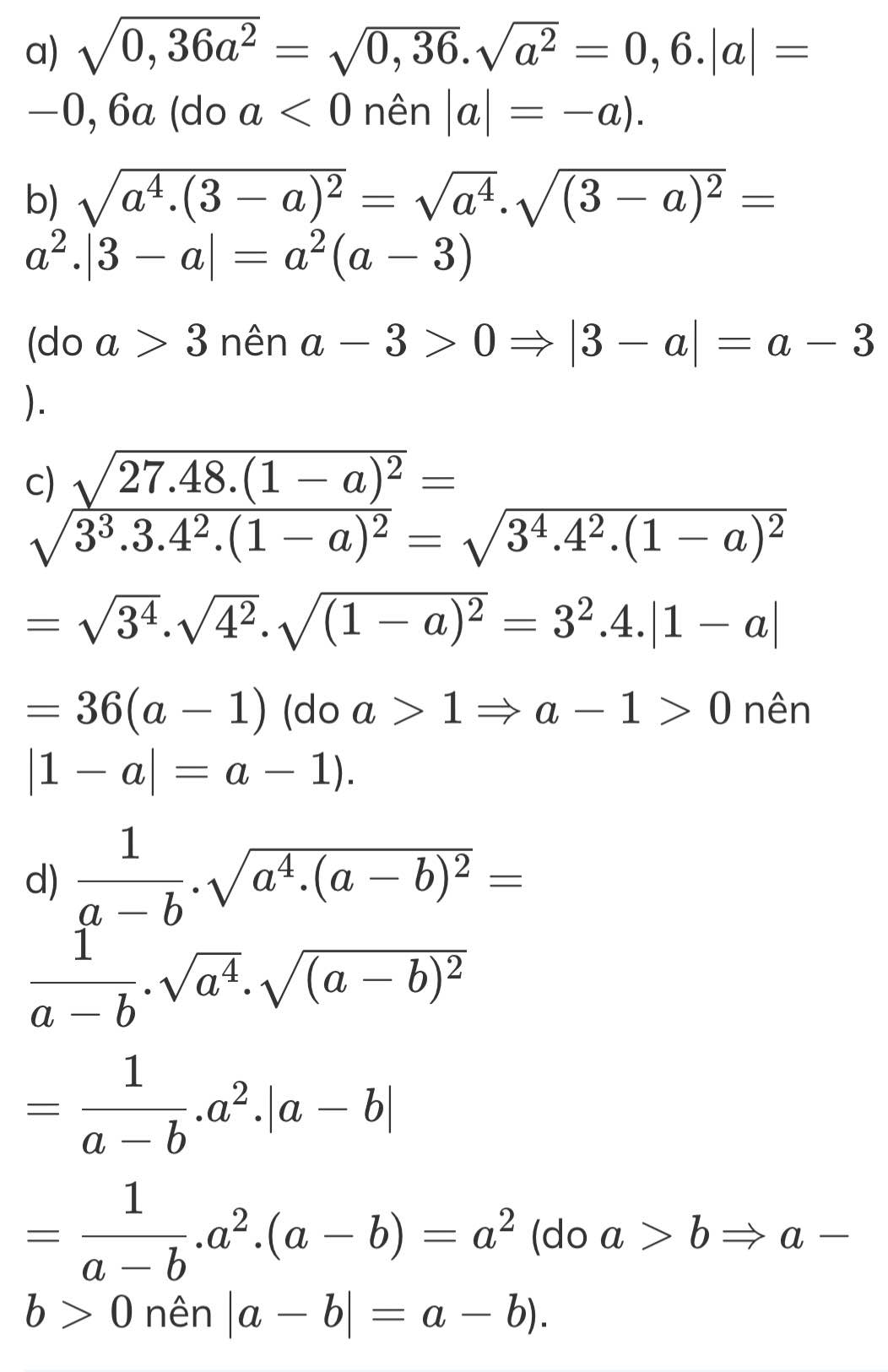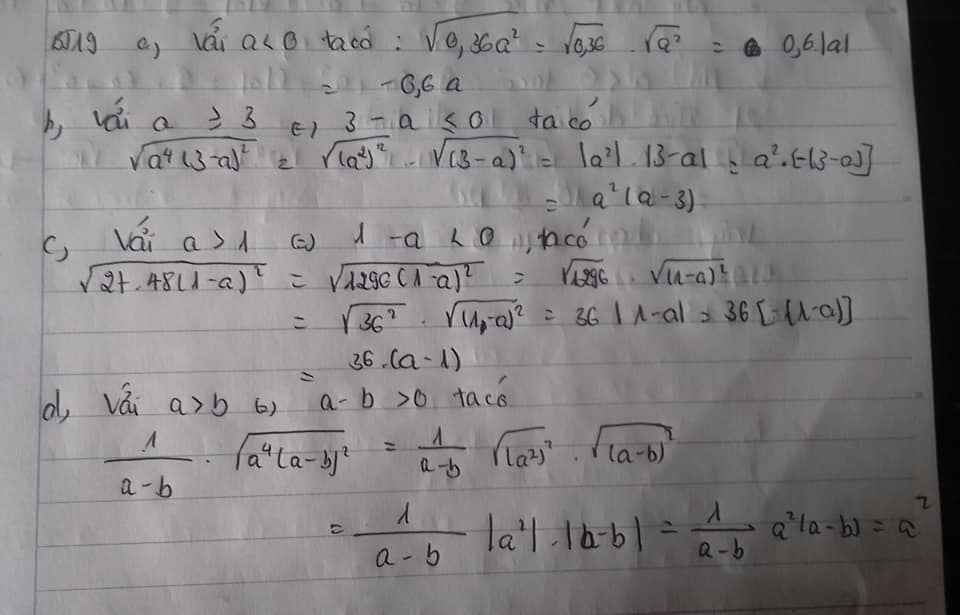Question

Bài 19 (trang 15 SGK Toán 9 Tập 1) 

Rút gọn các biểu thức sau:

a) $\sqrt{0,36.a^2}$ với $a<0$ ;                               b) $\sqrt{a^4.(3-a)^2}$ với $a \ge 3$ ;

c) $\sqrt{27.48.(1-a)^2}$ với $a>1$ ;                   d) $\dfrac{1}{a-b}.\sqrt{a^4.(a-b)^2}$ với $a>b$.

Answer 1

Bạn học tốt nhé

Answer 2

a)0,6.a

b)\(a^2\).(a-3)

c)36.(a-1)

d)\(\dfrac{1.a^2}{a-b}\).(a-b)

Answer 3

a) $\sqrt{0,36a^2}=\sqrt{0,36}.\sqrt{a^2}=0,6.|a|=-0,6a$ (do $a<0$ nên $|a|=-a$).

b) $\sqrt{a^4.(3-a{)}^2}=\sqrt{a^4}.\sqrt{(3-a{)}^2}=a^2.|3-a|=a^2(a-3)$

(do $a>3$ nên $a-3>0$ $\Rightarrow$ $|3-a|=a-3$).

c) $\sqrt{\mathrm{27.48.}(1-a{)}^2}=\sqrt{3^3.3{.4}^2.(1-a{)}^2}=\sqrt{3^4{.4}^2.(1-a{)}^2}$

$=\sqrt{3^4}.\sqrt{4^2}.\sqrt{(1-a{)}^2}=3^2.4.|1-a|$

$=36(a-1)$ (do $a>1$ $\Rightarrow$ $a-1>0$ nên $|1-a|=a-1$).

1a−b.a4.(a−b)2=1a−b.a4.(a−b)2

1a−b.a2.|a−b|

1a−b.a2.(a−b)=a2 (do $a>b$ $\Rightarrow$ $a-b>0$ nên $|a-b|=a-b$

Answer 4

a) -0,6a

b)  a^2(a-3)

c) 36(a-1)

d) a^2

Answer 5

 

a) Ta có:

$\sqrt{0,36a^2}=\sqrt{0,36}.\sqrt{a^2}$ 

                 $=\sqrt{0,6^2}.\sqrt{a^2}$

                 $=0,6.│a│$

                 $=0,6.(-a)=-0,6a$

(Vì $a<0$ nên $│a│=-a)$.

b) 

Vì $a^2$ ≥ 0   nên  $\left|a^2\right|=a^2$.

Vì $a\ge 3$   hay  $3\le a$   nên   $3-a\le 0$.

       $\Rightarrow │3-a│=-(3-a)=-3+a=a-3$.

Ta có: $\sqrt{a^4.(3-a{)}^2}=\sqrt{a^4}$.$\sqrt{(3-a{)}^2}$ 

                                         $=\sqrt{(a^2{)}^2}.\sqrt{(3-a{)}^2}$

                                         $=\left|a^2\right|.\left|3-a\right|$.

                                         $=a^2.(a-3)=a^3-3a^2$.

c) 

Vì $a>1$   hay   $1<a$    nên   $1-a<0$.

$\Rightarrow \left|1-a\right|=-(1-a)=-1+a=a-1$.

 Ta có: $\sqrt{27.48(1-a{)}^2}=\sqrt{27.\left(3.16\right).(1-a{)}^2}$

                                            $=\sqrt{\left(27.3\right).16.(1-a{)}^2}$

                                            $=\sqrt{\mathrm{81.16.}(1-a{)}^2}$ 

                                            $=\sqrt{81}.\sqrt{16}.\sqrt{{(1-a)}^2}$

                                            $=\sqrt{9^2}.\sqrt{4^2}.\sqrt{(1-a{)}^2}$

                                            $=\mathrm{9.4.}\left|1-a\right|=36.\left|1-a\right|$

                                             $=36.(a-1)=36a-36$.

d) 

Vì $a^2\ge 0$, với mọi $a$   nên $\left|a^2\right|=a^2$.

 Vì $a>b$ nên $a-b>0$. Do đó  $\left|a-b\right|=a-b$.

1a−b . $\sqrt{a^4.(a-b{)}^2}$

1a−b . $\sqrt{a^4}.\sqrt{(a-b{)}^2}$

1a−b.|a2|.|a−b|

1a−b.a2.(a−b)

$=a^2$

 

Answer 6

Answer 7

a) $\sqrt{0,36a^2}=\sqrt{0,36}.\sqrt{a^2}=0,6.|a|=-0,6a$ (do $a<0$ nên $|a|=-a$).

b) $\sqrt{a^4.(3-a{)}^2}=\sqrt{a^4}.\sqrt{(3-a{)}^2}=a^2.|3-a|=a^2(a-3)$

(do $a>3$ nên $a-3>0$ $\Rightarrow$ $|3-a|=a-3$).

c) $\sqrt{\mathrm{27.48.}(1-a{)}^2}=\sqrt{3^3.3{.4}^2.(1-a{)}^2}=\sqrt{3^4{.4}^2.(1-a{)}^2}$

$=\sqrt{3^4}.\sqrt{4^2}.\sqrt{(1-a{)}^2}=3^2.4.|1-a|$

$=36(a-1)$ (do $a>1$ $\Rightarrow$ $a-1>0$ nên $|1-a|=a-1$).

d) $\frac{1}{a-b}.\sqrt{a^4.(a-b{)}^2}=\frac{1}{a-b}.\sqrt{a^4}.\sqrt{(a-b{)}^2}$

$=\frac{1}{a-b}.a^2.|a-b|$

$=\frac{1}{a-b}.a^2.(a-b)=a^2$ (do $a>b$ $\Rightarrow$ $a-b>0$ nên 

Answer 8

a) \(\sqrt{0,36.a^2}=\)-0,6.a

b) \(\sqrt{a^4.\left(3-a\right)^2}=a^2.\left(a-3\right)\)

c) \(\sqrt{27.48.\left(1-a\right)^2}=36.\left(a-1\right)\)

d) \(\dfrac{1}{a-b}.\sqrt{a^4.\left(a-b\right)^2}=a^2\)

Answer 9

Answer 10

a) \(\sqrt{0,36.a^2}=0,6\left(-a\right)\)

b) \(\sqrt{a^4.\left(3-a\right)^2}=a^2.\left(a-3\right)\)

c) \(\sqrt{27.48.\left(1-a\right)^2}=\sqrt{9.3.3.16.\left(1-a\right)^2}=3.3.4\left(a-1\right)=36\left(a-1\right)\)

d) \(\dfrac{1}{a-b}\sqrt{a^4\left(a-b\right)^2}=\dfrac{1}{a-b}.a^2.\left(a-b\right)=a^2\)

Answer 11

Answer 12

Answer 13

Answer 14

Answer 15

Answer 16

a) -0.6a
b) a²(a - 3)
c) 36(a - 1)
d) a²

Answer 17

Answer 18

a) $-0,6a$ (do $a<0$ nên $|a|=-a$).

b) 

a2(a−3)

(do $a>3$ nên $a-3>0$ $\Rightarrow$ $|3-a|=a-3$).

c) $36(a-1)$ (do $a>1$ $\Rightarrow$ $a-1>0$ nên $|1-a|=a-1$).

d) a2 (do $a>b$ $\Rightarrow$ $a-b>0$ nên $|a-b|=a-b$).

 

Answer 19

Answer 20

\(\sqrt{0,36.a^2}=\sqrt{\left(0,6.a\right)^2}=|0,6.a|=-0,6a\)

 

Answer 21

Answer 22

a,\(\sqrt{0,36a^2}\)=\(\sqrt{0,36}\).\(\sqrt{a^2}\)=0,6.|a| =-0,6|a| ( do a<0 nên |a|=-a)

b,\(\sqrt{a^4.\left(3-a\right)^2}\)= \(\sqrt{\left(a^2\right)}^2\).\(\sqrt{\left(3-a\right)}^2\)=a\(^2\). |3-a| =a\(^2\).(a-3) 

(do a>3 nên a-3 >0 => |a-3| = a-3 )

c,\(\sqrt{27.48.\left(1-a^{ }\right)^2}\)=\(\sqrt{3^3.3.4^2.\left(1-a^{ }\right)^2}\)= \(\sqrt{3^4.4^2.\left(1-a\right)^2}\)=\(\sqrt{3^4}\).\(\sqrt{4^2}\)\(\sqrt{\left(1-a^{ }\right)^2}\)=3\(^2\).4|1-a|=36.(a-1)( do a>1 => a-1>0 nên |a-1| = a-1

d,\(\dfrac{1}{a-b}\).\(\sqrt{a^4.\left(a-b^{ }\right)^2}\)=\(\dfrac{1}{a-b}\).\(\sqrt{a^4}\).\(\sqrt{\left(a-b\right)^2}\)= \(\dfrac{1}{a-b}\). a\(^2\).|a-b|= \(\dfrac{1}{a-b}\).a\(^2\).(a-b) = a\(^2\)( do a>b => a-b >0 nên |a-b| = a-b

Answer 23

a=-0,6
b=a²(a-3)
c=a-1
d=a-b

Answer 24

Answer 25

a)\(\sqrt{0,36a^2}\) với a<0
=\(\left|0,6a\right|\)=\(-\left|0,6a\right|\) (vì a<0)
b) \(\sqrt{a^4.\left(3-a\right)^2}\) với a\(\ge\)3
=\(\sqrt{a^4}.\sqrt{\left(3-a\right)^2}\)
=\(\left|a^2\right|.\left|3-a\right|\)
=\(\left\{{}\begin{matrix}a.\left(a-3\right)=a^2-3a\left(a>3\right)\\0\left(a=3\right)\end{matrix}\right.\)
c) \(\sqrt{27.48\left(1-a\right)^2}\) với a>1
=\(\sqrt{27.48}.\sqrt{\left(1-a\right)^2}\)
=\(\sqrt{1296}.\left|1-a\right|\)
=\(36.\left(a-1\right)\) (vì a>1 ⇒1-a<0)
=\(-36+36a\)
d) \(\dfrac{1}{a-b}.\sqrt{a^4.\left(a-b\right)^2}\) với a>b
=\(\dfrac{1}{a-b}.\sqrt{a^4}.\sqrt{\left(a-b\right)^2}\)
=\(\dfrac{1}{a-b}.\left|a^2\right|.\left|a-b\right|\)
=\(\dfrac{1}{a-b}.a^2.\left(a-b\right)\) (vì a ≥ 0 ∀x ; a>b ⇒a-b >0)
=\(a^2\)

Answer 26

a,\(\sqrt{0,36.a^2}\) với a < 0

= \(|0,6a|=-0,6a\) ( vì a < 0 )

b,\(\sqrt{a^4.\left(3-a\right)^2}\)  với a ≥ 3

=\(a^2|3-a|\) = \(a^2\left(3-a\right)\) ( vì a ≥ 3 ⇒ a-3 ≥ 3)

c,\(\sqrt{27.49.\left(1-a\right)^2}\) với a > 1

=\(\sqrt{9.3.3.16.\left(1-a\right)^2}\)

=\(\sqrt{36^2}.\sqrt{\left(1-a\right)^2}\)=\(36|1-a|\)\(=36\left(a-1\right)\) ( vì a > 1 ⇒ a-1 >1 )

d,\(\dfrac{1}{a-b}.\sqrt{a^4.\left(a-b\right)^2}\) với a > b

=\(\dfrac{1}{a-b}.a^2|a-b|\)

=\(\dfrac{1}{a-b}.a^2\left(a-b\right)\) \(=a^2\) ( vì a > b ⇒ a-b > 0)

 

Answer 27

 $\sqrt{0,36a^2}=\sqrt{0,36}.\sqrt{a^2}=0,6.|a|=-0,6a$ (do $a<0$ nên $|a|=-a$).

b) $\sqrt{a^4.(3-a{)}^2}=\sqrt{a^4}.\sqrt{(3-a{)}^2}=a^2.|3-a|=a^2(a-3)$

(do $a>3$ nên $a-3>0$ $\Rightarrow$ $|3-a|=a-3$).

c) $\sqrt{\mathrm{27.48.}(1-a{)}^2}=\sqrt{3^3.3{.4}^2.(1-a{)}^2}=\sqrt{3^4{.4}^2.(1-a{)}^2}$

$=\sqrt{3^4}.\sqrt{4^2}.\sqrt{(1-a{)}^2}=3^2.4.|1-a|$

$=36(a-1)$ (do $a>1$ $\Rightarrow$ $a-1>0$ nên $|1-a|=a-1$).

1a−b.a4.(a−b)2=1a−b.a4.(a−b)2

1a−b.a2.|a−b|

1a−b.a2.(a−b)=a2 (do $a>b$ $\Rightarrow$ $a-b>0$ nên $|a-b|=a-b$).

Answer 28

a) \(\sqrt{0,36.a^2}=\left|0,6\right|=-0,6\left(via< 0\Rightarrow0,6a< 0\right)\)

b)\(\sqrt{a^4.\left(3-a\right)^2}=\sqrt{a^4}.\sqrt{\left(3-a\right)^2}=\left|a^2\right|.\left|3-a\right|=a^2.\left(a-3\right)\left(via\ge3\Rightarrow3-a\ge0\right)\)

c)\(\sqrt{27.48.\left(1-a\right)^2}=\sqrt{1296.\left(1-a\right)^2}=\sqrt{1296}.\sqrt{\left(1-a\right)^2}=36.\left|1-a\right|=36.\left(a-1\right)\left(via>1\right)\)

d)\(\dfrac{1}{a-b}.\sqrt{a^4.\left(a-b\right)^2}=\dfrac{1}{a-b}.\sqrt{\left(a^2\right)^2}.\sqrt{\left(a-b\right)^2}=\dfrac{1}{a-b}.\left|a^2\right|.\left|a-b\right|=\dfrac{1}{a-b}.a^2.(a-b)=a^2\left(via>0\Rightarrow a-b>0\right)\)

Answer 29

a) \sqrt{0,36a^2}=\sqrt{0,36}.\sqrt{a^2}=0,6.|a|=-0,6a 0,36a 2 ​ = 0,36 ​ . a 2 ​ =0,6.∣a∣=−0,6a (do a<0a<0 nên |a|=-a∣a∣=−a). b) \sqrt{a^4.(3-a)^2}=\sqrt{a^4}.\sqrt{(3-a)^2}=a^2.|3-a|=a^2(a-3) a 4 .(3−a) 2 ​ = a 4 ​ . (3−a) 2 ​ =a 2 .∣3−a∣=a 2 (a−3) (do a>3a>3 nên a-3>0a−3>0 \Rightarrow⇒ |3-a|=a-3∣3−a∣=a−3). c) \sqrt{27.48.(1-a)^2}=\sqrt{3^3.3.4^2.(1-a)^2}=\sqrt{3^4.4^2.(1-a)^2} 27.48.(1−a) 2 ​ = 3 3 .3.4 2 .(1−a) 2 ​ = 3 4 .4 2 .(1−a) 2 ​ =\sqrt{3^4}.\sqrt{4^2}.\sqrt{(1-a)^2}=3^2.4.|1-a|= 3 4 ​ . 4 2 ​ . (1−a) 2 ​ =3 2 .4.∣1−a∣ =36(a-1)=36(a−1) (do a>1a>1 \Rightarrow⇒ a-1>0a−1>0 nên |1-a|=a-1∣1−a∣=a−1). d) \dfrac{1}{a-b}.\sqrt{a^4.(a-b)^2}=\dfrac{1}{a-b}.\sqrt{a^4}.\sqrt{(a-b)^2} a−b 1 ​ . a 4 .(a−b) 2 ​ = a−b 1 ​ . a 4 ​ . (a−b) 2 ​ =\dfrac{1}{a-b}.a^2.|a-b|= a−b 1 ​ .a 2 .∣a−b∣ =\dfrac{1}{a-b}.a^2.(a-b)=a^2= a−b 1 ​ .a 2 .(a−b)=a 2 (do a>ba>b \Rightarrow⇒ a-b>0a−b>0 nên |a-b|=a-b∣a−b∣=a−b).

Answer 30

a) $\sqrt{0,36a^2}=\sqrt{0,36}.\sqrt{a^2}=0,6.|a|=-0,6a$(do $a<0$ nên $|a|=-a$).

b) $\sqrt{a^4.(3-a{)}^2}=\sqrt{a^4}.\sqrt{(3-a{)}^2}=a^2.|3-a|=a^2(a-3)$

(do $a>3$ nên $a-3>0$ $\Rightarrow$ $|3-a|=a-3$).

c) $\sqrt{\mathrm{27.48.}(1-a{)}^2}=\sqrt{3^3.3{.4}^2.(1-a{)}^2}=\sqrt{3^4{.4}^2.(1-a{)}^2}$

$=\sqrt{3^4}.\sqrt{4^2}.\sqrt{(1-a{)}^2}=3^2.4.|1-a|$

$=36(a-1)$ (do $a>1$ $\Rightarrow$ $a-1>0$ nên $|1-a|=a-1$).

1a−b.a4.(a−b)2=1a−b.a4.(a−b)2

1a−b.a2.|a−b|

1a−b.a2.(a−b)=a2 (do $a>b$ $\Rightarrow$ $a-b>0$ nên $|a-b|=a-b$).