Question

Bài 15 (trang 106 SGK Toán 9 Tập 1)

Cho hình 70 trong đó hai đường tròn cùng có tâm là O. Cho biết AB > CD.

Hãy so sánh các độ dài:

a) OH và OK

b) ME và MF

c) MH và MK.

Answer 1

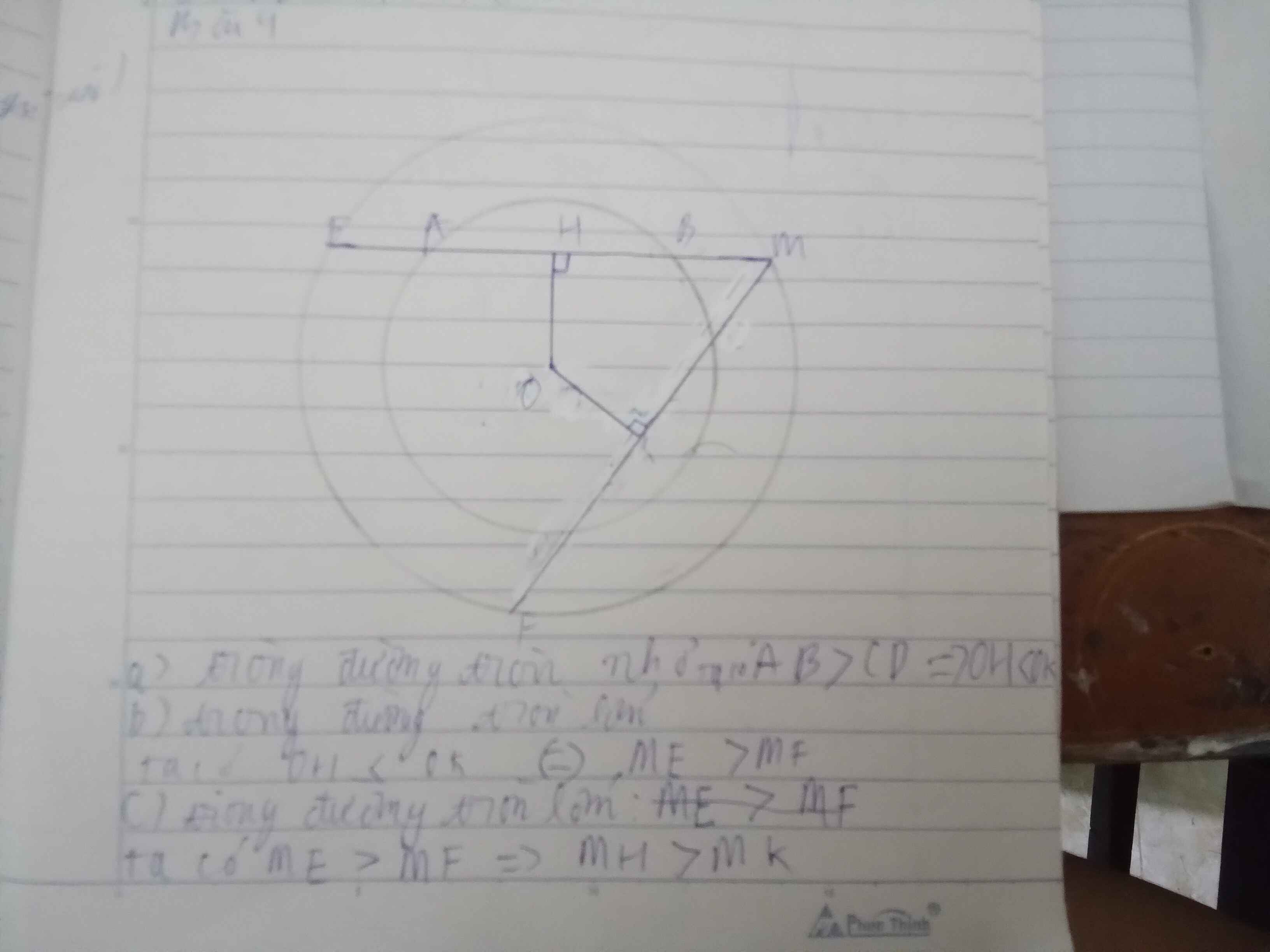
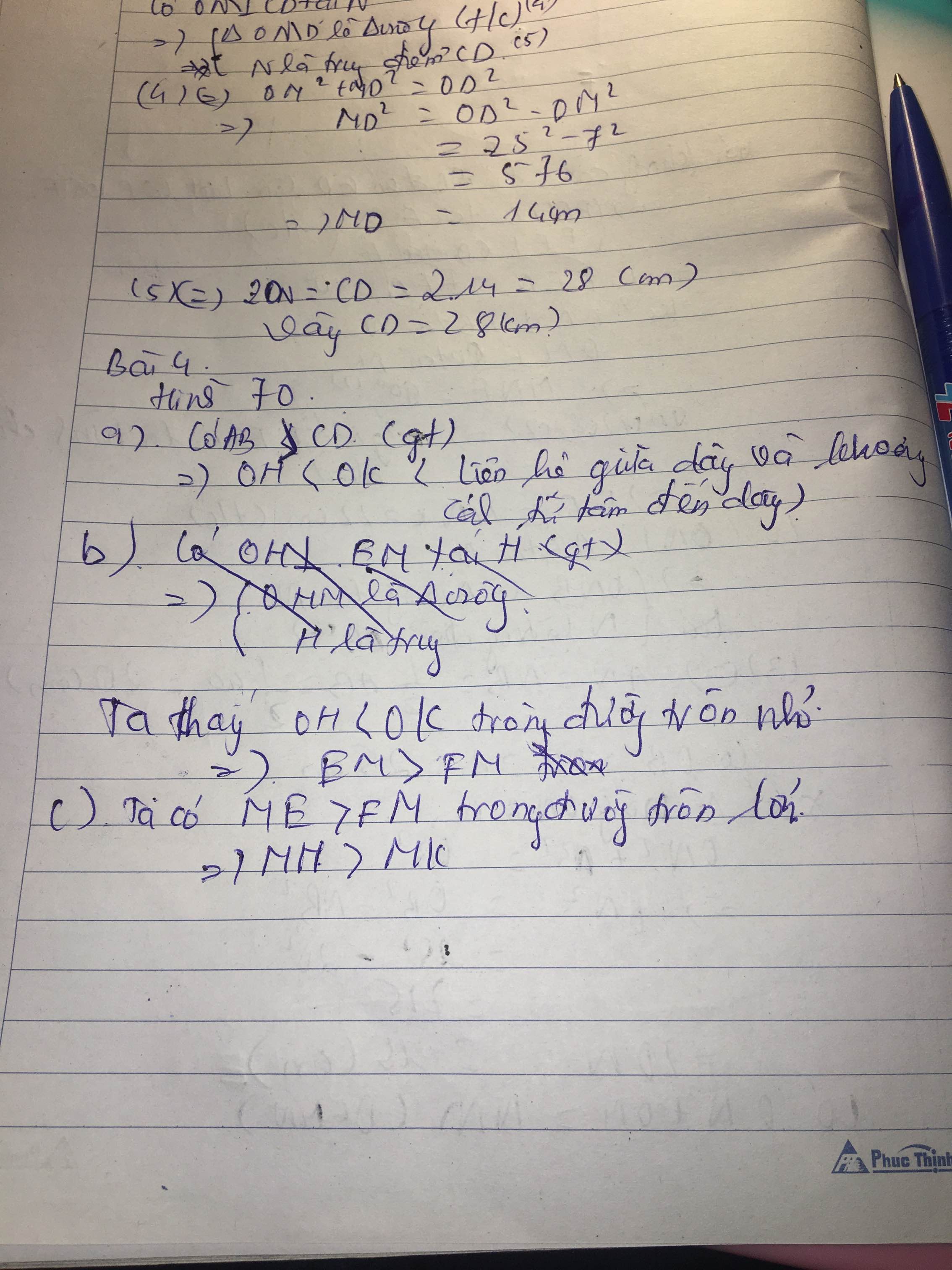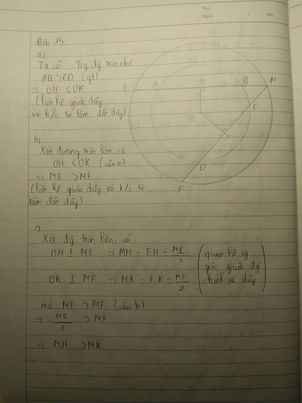a) Trong đường tròn nhỏ:

AB > CD => OH < OK (định lí 3)

b) Trong đường tròn lớn:

OH < OK => ME > MF (định lí 3)

c) Trong đường tròn lớn:

ME > MF => MH > MK

Answer 2

ME2" role="presentation" style="border:0px; direction:ltr; display:inline-block; float:none; font-size:19.2px; line-height:0; margin:0px; max-height:none; max-width:none; min-height:0px; min-width:0px; overflow-wrap:normal; padding:1px 0px; position:relative; white-space:nowrap; word-spacing:normal" class="MathJax_CHTML mjx-chtml">ME2 (Định lý 2 - trang 103).

MF2" role="presentation" style="border:0px; direction:ltr; display:inline-block; float:none; font-size:19.2px; line-height:0; margin:0px; max-height:none; max-width:none; min-height:0px; min-width:0px; overflow-wrap:normal; padding:1px 0px; position:relative; white-space:nowrap; word-spacing:normal" class="MathJax_CHTML mjx-chtml">MF2 (Định lý 2 - trang 103). 

ME2&gt;MF2&#x21D4;MH&gt;MK" role="presentation" style="border:0px; direction:ltr; display:inline-block; float:none; font-size:19.2px; line-height:0; margin:0px; max-height:none; max-width:none; min-height:0px; min-width:0px; overflow-wrap:normal; padding:1px 0px; position:relative; white-space:nowrap; word-spacing:normal" class="MathJax_CHTML mjx-chtml">ME>MF⇒ME2>MF2⇔MH>MK

Answer 3

a) Trong đường tròn nhỏ: $AB>CD$ $\Rightarrow$ $OH<OK$.

b) Trong đường tròn lớn : $OH<OK$ $\Rightarrow$ $ME>MF$.

c) Trong đường tròn lớn : $ME>MF$ $\Rightarrow$ $MH>MK$.

Answer 4

a) Trong đường tròn nhỏ: $AB>CD$ $\Rightarrow$ $OH<OK$.

b) Trong đường tròn lớn : $OH<OK$ $\Rightarrow$ $ME>MF$.

c) Trong đường tròn lớn : $ME>MF$ $\Rightarrow$ $MH>MK$.

Answer 5

ta có ab lớn hơn cd suy ra oh nhỏ hơn ok

b) ta có oh nhỏ hơn ok nên me lớn hơn mf

c) ta có me lơn hơn mf nên suy ra mh lớn hơn mk

 

Answer 6

a) Trong đường tròn nhỏ: $AB>CD$ $\Rightarrow$ $OH<OK$.

b) Trong đường tròn lớn : $OH<OK$ $\Rightarrow$ $ME>MF$.

c) Trong đường tròn lớn : $ME>MF$ $\Rightarrow$ $MH>MK$

 

Answer 7

a) Xét trong đường tròn nhỏ:

Theo định lí $2$: trong hai dây của một đường tròn, dây nào lớn hơn thì dây đó gần tâm hơn.

Theo giả thiết $AB>CD$ suy ra $AB$ gần tâm hơn, tức là  $OH<OK$.

b) Xét trong đường tròn lớn:

Theo định lí $2$: trong hai dây của một đường tròn, dây nào gần tâm hơn thì dây đó lớn hơn.

Theo câu $a$, ta có: $OH<OK\Rightarrow ME>MF$.

c) Xét trong đường tròn lớn:

ME2 (Định lý 2 - trang 103).

MF2 (Định lý 2 - trang 103). 

ME>MF⇒ME2>MF2⇔MH>MK

 

Answer 8

a) Trong đường tròn nhỏ: $AB>CD$ $\Rightarrow$ $OH<OK$.

b) Trong đường tròn lớn : $OH<OK$ $\Rightarrow$ $ME>MF$.

c) Trong đường tròn lớn : $ME>MF$ $\Rightarrow$ $MH>MK$.

Answer 9

  

Answer 10

  

Answer 11

  

Answer 12

 

Answer 13

  

Answer 14

                                                               GIẢI

a,   Xét (O;OA) có:

           AB > CD (gt)

⇒   OH < OK (ĐL)

b,  Xét (O;OM) có:

          OH < OK (cmt)

⇒   ME > MF (ĐL)

c,  Xét (O;OM) có:

          OH\(\perp\)ME tại H (gt)

⇒  H là trung điểm của ME (ĐL)

⇒  MH = \(\dfrac{ME}{2}\) (đn)

    CMTT có: MK = \(\dfrac{MF}{2}\) (đn)

    Mà ME > MF (cmt)

⇒ MH > MK 

Answer 15

a) OH<OK

b) ME>MF

c) MH>MK

Answer 16

 

Answer 17

a) 

xét đường tròn nhỏ (O) có AB>CD=> OH<OK ( ĐỊNH LÝ 2)

b)  xét  đường tròn lớn (O) có  OK>OH => MF<ME (3) ( ĐỊNH LÝ 2)

c) vì đường tròn lớn (O) có

OH⊥EM => EH=MH=EM/2 (1)

CMTT CÓ OK⊥FM => FK=MK=FM/2 (2)

TỪ (1) (2) (3) =>MH>MK

                                                

 

Answer 18

Trong đường tròn nhỏ: 

AB > CD => OH < OK (định lí 3)

b) Trong đường tròn lớn:

OH < OK => ME > MF (định lí 3)

c) Trong đường tròn lớn:

ME > MF => MH > MK

Answer 19

 

Answer 20

 

Answer 21

a, Trong hình tròn nhỏ

AB lớn hơn CD ⇒ OH nhỏ hơn OK ( định lí 3 )

b, Trong đường tròn lớn 

OH nhỏ hơn OK ⇒ ME lớn hơn MF

c, Trong đường tròn lớn 

ME nhỏ hơn MF ⇒ MH lớn hơn MK 

Answer 22

a, Trong hình tròn nhỏ ta có 

AB > CD ⇒ OH < OK ( định lí 3 ) 

b, Trong đường tròn lớn tao có 

OH < OK ⇒ ME > MF 

c, Trong đường tròn lớn ta có 

ME < MF ⇒ MH > MK 

###myduyen

Answer 23

a.Xét đường tròn O có AB>CD =>OH=OK b Xét đường tròn O có OH>OK =>Me>MF c Xét đường tròn O có OH vuông góc ME =>MH=1/2ME Ta lại có:MK=1/2MF Mà ME>MF =>MH>MK(Đpcm)

Answer 24

Answer 25

a) Trong đường trong nhỏ:

AB > CD => OH < OK( DL 3)

b) Trong đg trong lớn:

OH < OK => ME > MF(DL 3)

c) Trong dg tròn lớn:

ME > MF = MH > MK

 

Answer 26

a) Trong đường tròn nhỏ:

AB > CD => OH < OK (định lí 3)

b) Trong đường tròn lớn:

OH < OK => ME > MF (định lí 3)

c) Trong đường tròn lớn:

ME > MF => MH > MK

Answer 27

 

Answer 28

a) Xét trong đường tròn nhỏ:

Theo định lí $2$: trong hai dây của một đường tròn, dây nào lớn hơn thì dây đó gần tâm hơn.

Theo giả thiết $AB>CD$ suy ra $AB$ gần tâm hơn, tức là  $OH<OK$.

b) Xét trong đường tròn lớn:

Theo định lí $2$: trong hai dây của một đường tròn, dây nào gần tâm hơn thì dây đó lớn hơn.

Theo câu $a$, ta có: $OH<OK\Rightarrow ME>MF$.

c) Xét trong đường tròn lớn:

ME2 (Định lý 2 - trang 103).

MF2 (Định lý 2 - trang 103). 

ME>MF⇒ME2>MF2⇔MH>MK

Answer 29

a) Trong đường tròn nhỏ: $AB>CD$ $\Rightarrow$ $OH<OK$.

b) Trong đường tròn lớn : $OH<OK$ $\Rightarrow$ $ME>MF$.

c) Trong đường tròn lớn : $ME>MF$ $\Rightarrow$ $MH>MK$.

Answer 30

a