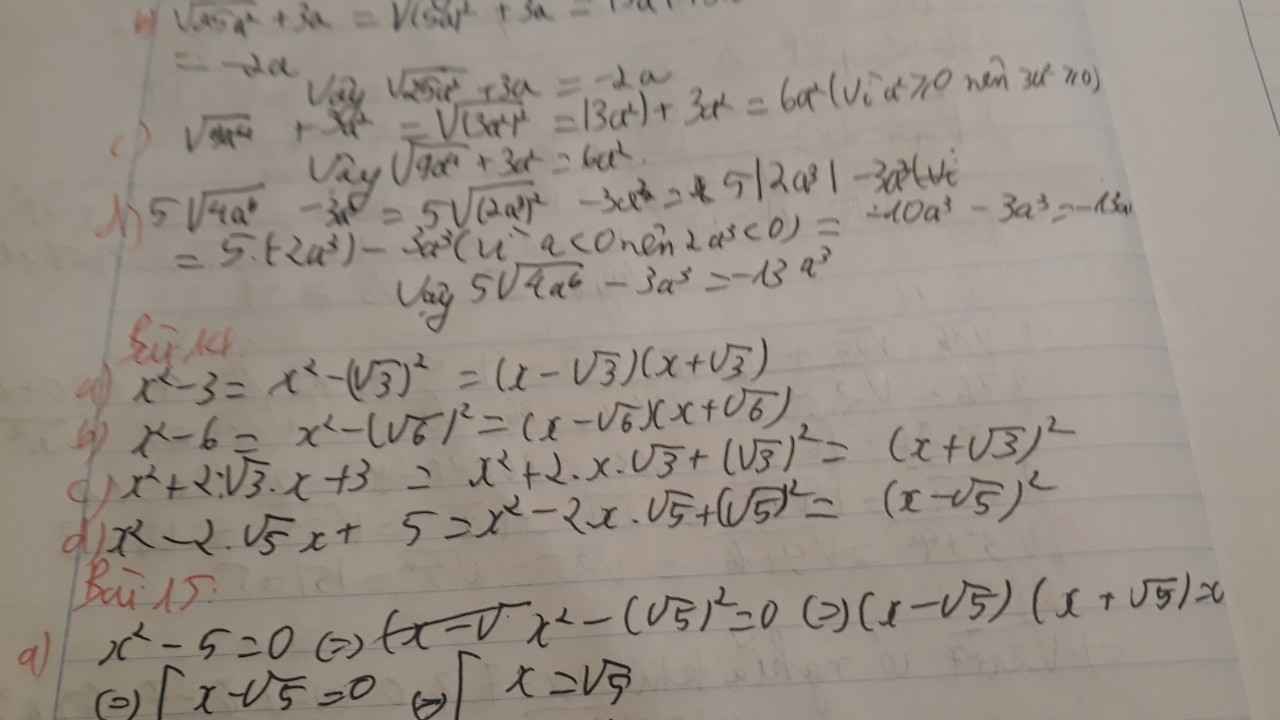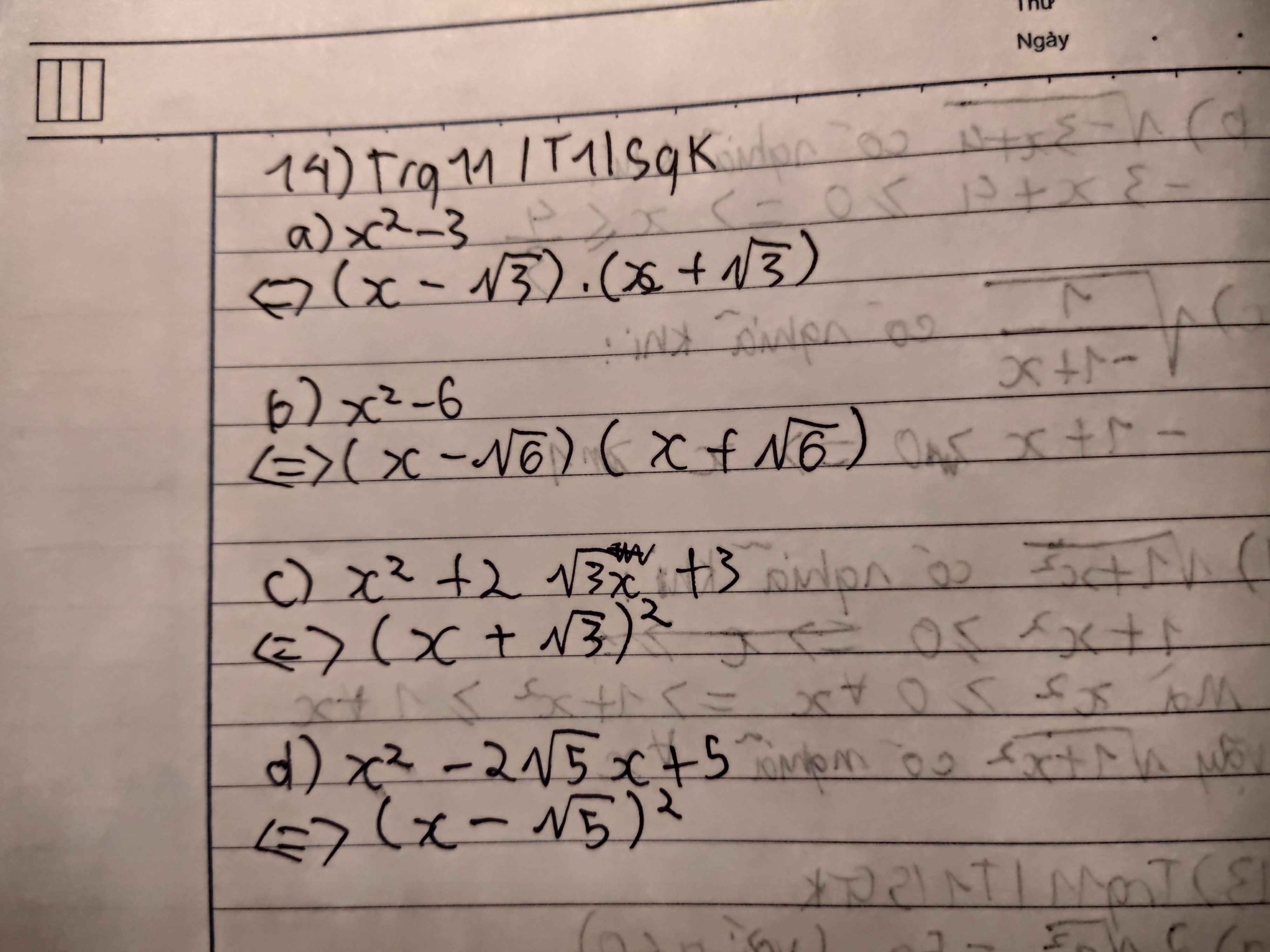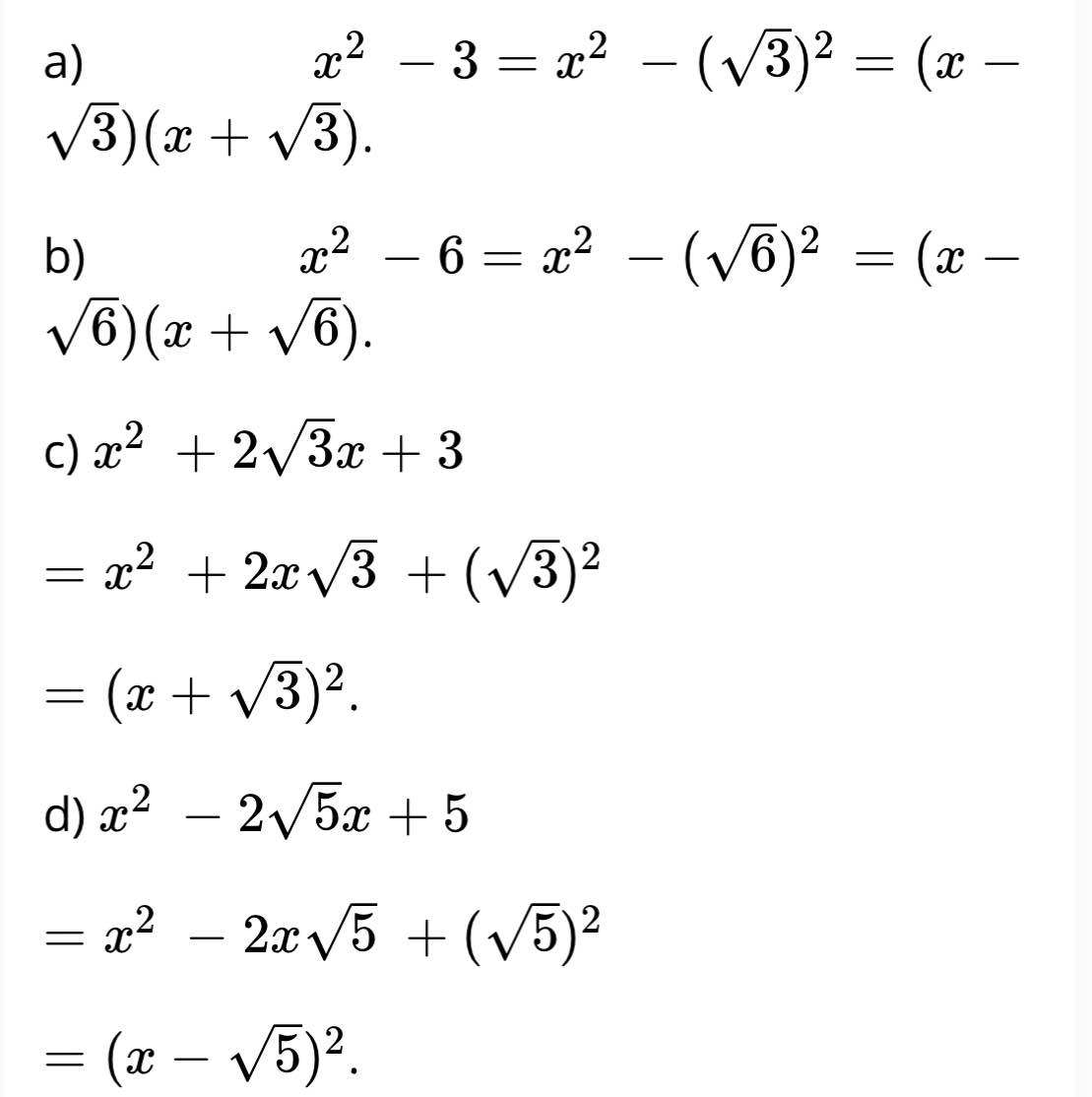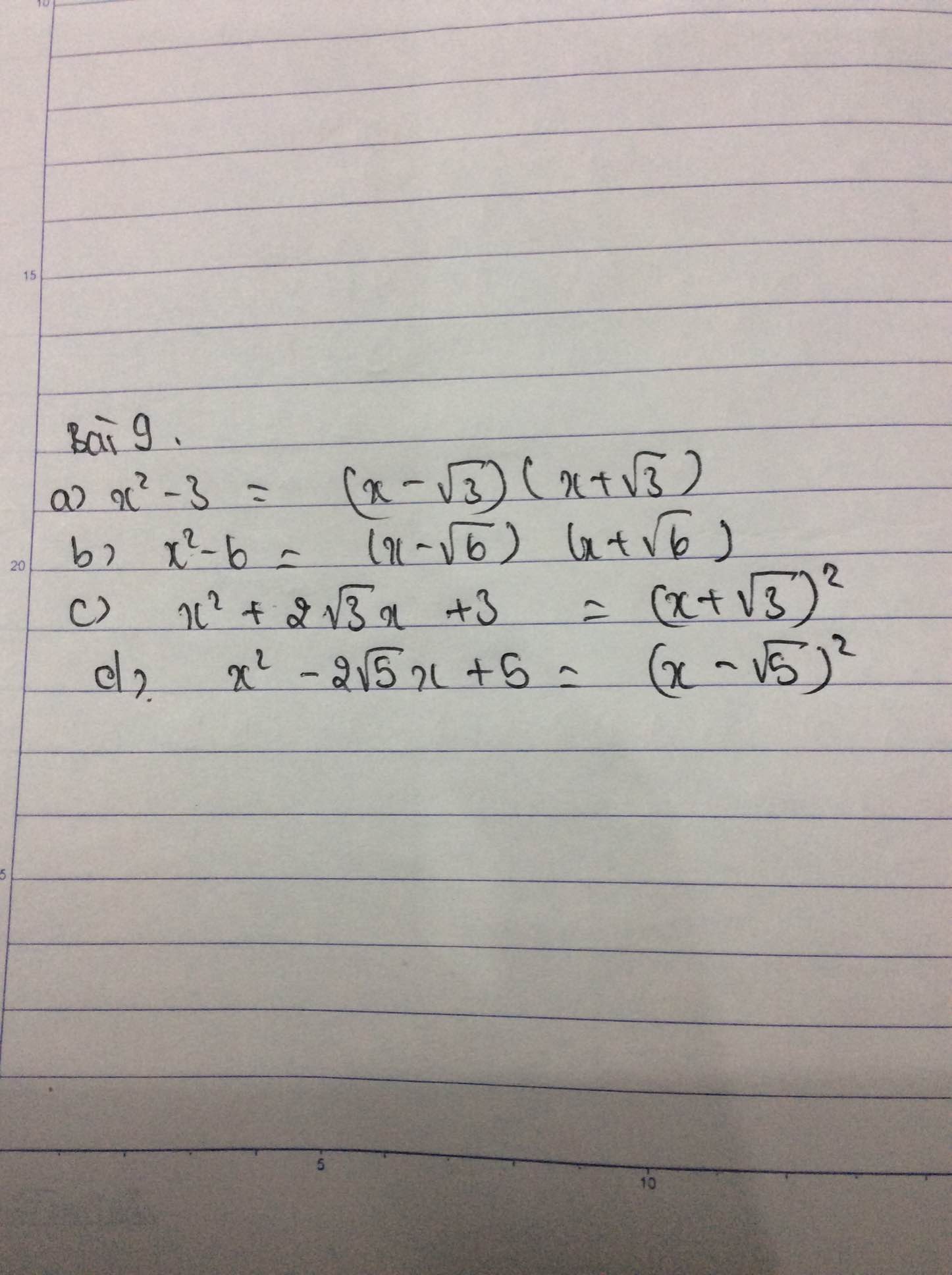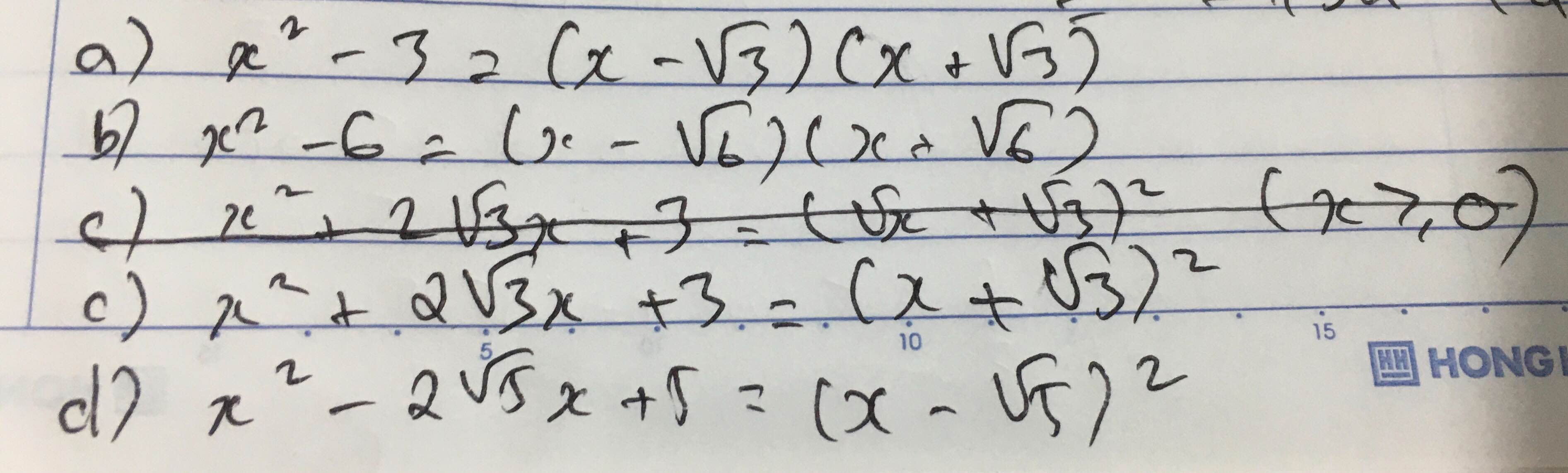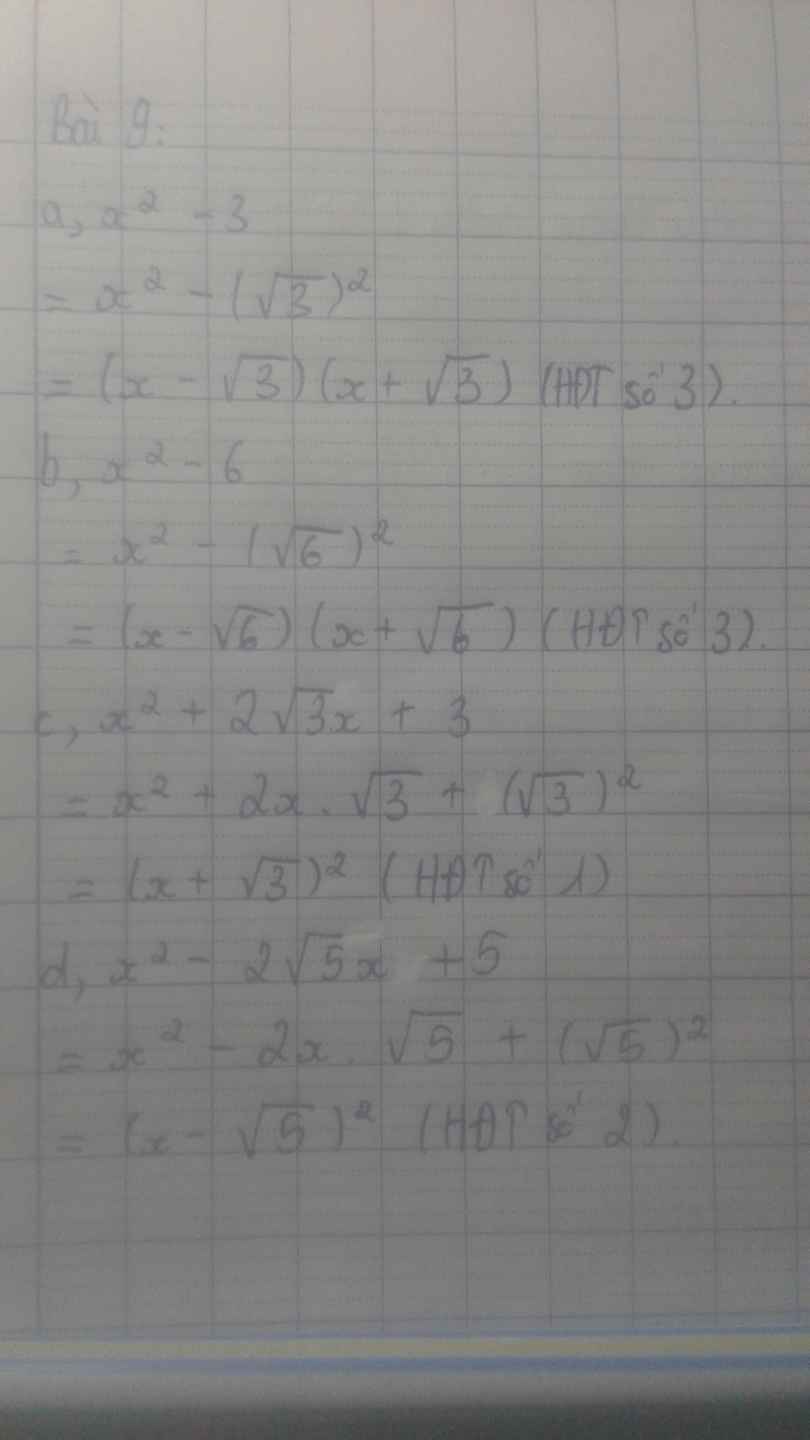a, \(x^2-3=\left(x-\sqrt{3}\right)\left(x+\sqrt{3}\right)\)
b, \(x^2-6=\left(x-\sqrt{6}\right)\left(x+\sqrt{6}\right)\)
c, \(x^2+2\sqrt{3}+3=x^2+2\sqrt{3}+\left(\sqrt{3}\right)^2=\left(x+\sqrt{3}\right)^2\)
d, \(x^2-2\sqrt{5}x+5=x^2-2\sqrt{5}x+\left(\sqrt{5}\right)^2=\left(x-\sqrt{5}\right)^2\)
a) \(x^2\) - 3 = (x-\(\sqrt{3}\))(x+\(\sqrt{3}\))
b)\(x^2\)-6=(x-\(\sqrt{6}\))(x+\(\sqrt{6}\))
c) \(x^2+2\sqrt{3}x+3\)= \(\left(x+\sqrt{3}\right)^2\)
d) \(x^2-2\sqrt{5}x+5\)=\(\left(x-\sqrt{5}\right)^2\)
a, ( x^2- √3).(x^2+ √3)
b, (x^2- √6).(x^2+ √6)
c, (√x + √3)^2
d, ( √x - √5)^2
a) \(x^2-3=\left(x-\sqrt{3}\right)\left(x+\sqrt{3}\right)\)
b) \(x^2-6=\left(x-\sqrt{6}\right)\left(x+\sqrt{6}\right)\)
c) \(x^2+2\sqrt{3}x+3=\left(x+\sqrt{3}\right)^2\)
d) \(x^2-2\sqrt{5}x+5=\left(x-\sqrt{5}\right)^2\)
a) .
b) .
c)
.
d)
![]()
a. x2 - 3 = x2 - \(\left(\sqrt{3}\right)^2\) = (x - \(\sqrt{3}\) ) (x + \(\sqrt{3}\) )
b. x2 - 6 = x2 - (\(\sqrt{6}\))2 = ( x - \(\sqrt{6}\)) (x + \(\sqrt{6}\))
c. x2 + 2\(\sqrt{3}\)x + (\(\sqrt{3}\) )2
= x2 + 2x\(\sqrt{3}\) + (\(\sqrt{3}\) )2
= (x+ \(\sqrt{3}\) )2
d. x2 - 2\(\sqrt{5}\)x + 5
= x2 - 2x\(\sqrt{5}\) + (\(\sqrt{5}\) )2
= (x - \(\sqrt{5}\))2
a) = (x-\(\sqrt{3}\))(x+\(\sqrt{3}\))
b) = (x-\(\sqrt{6}\))(x+\(\sqrt{6}\))
c) = (x+\(\sqrt{3}\))2
d) = (x-\(\sqrt{5}\))2
a) .
b) .
c)
.
d)
.
a) .
b) .
c)
.
d)
.
a) Ta có:
b) Ta có:
c) Ta có:
d) Ta có:
a) Ta có:
b) Ta có:
c) Ta có:
d) Ta có:
a, x=7; x=-7
b, x=8; x=-8
c, x=3; x=-3
d, x=4; x=-4
a) x2 - 3 = x2 - ( \(\sqrt{3}\) )2 = ( x - \(\sqrt{3}\) )2 = ( x - \(\sqrt{3}\) )( x + \(\sqrt{3}\) )
b) x2 - 6 = x2 - ( \(\sqrt{6}\) )2 = ( x - \(\sqrt{6}\) )( x + \(\sqrt{6}\) )
c) x2 + 2.\(\sqrt{3}\).x + 3 = x2 + 2.\(\sqrt{3}\).x + \(\sqrt{3^2}\) = ( x + \(\sqrt{3}\) )2
d) x2 - 2\(\sqrt{5}\)x + 5 = x2 - 2\(\sqrt{5}\)x + \(\sqrt{5^2}\) = ( x - \(\sqrt{5}\) )2
a) x\(^2\) - 3 = x\(^2\) - (\(\sqrt{3}\) )\(^2\) = ( x - \(\sqrt{3}\) )( x + \(\sqrt{3}\) )
b) x\(^2\) - 6 = x\(^2\) - (\(\sqrt{6}\) )\(^2\) = ( x -\(\sqrt{6}\) )(x + \(\sqrt{6}\) )
c) x\(^2\) + 2\(\sqrt{3x}\) +3 = x\(^2\) + 2x\(\sqrt{3}\) + (\(\sqrt{3}\) )\(^2\) = ( x - \(\sqrt{5}\) )\(^2\)
d) x\(^2\) - 2\(\sqrt{5x}\) + 5 = x\(^2\) - 2\(\sqrt{5x}\) + (\(\sqrt{5}\) )\(^2\) = ( x - \(\sqrt{5}\) )\(^2\)
a) ( x- căn3)*(x+ căn 3)
b) ( x- căn 6)*(x+ căn 6)
c)(x+ căn 3)^2
d)(x- căn 5)^2
a, =x2-(\(\sqrt{3}\))2=(x-\(\sqrt{3}\))(x+\(\sqrt{3}\))
b,=x2-(\(\sqrt{6}\))2=(x-\(\sqrt{6}\))(x+\(\sqrt{6}\))
c,=(x+\(\sqrt{3}\))2
d,= (x+\(\sqrt{5}\))2