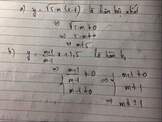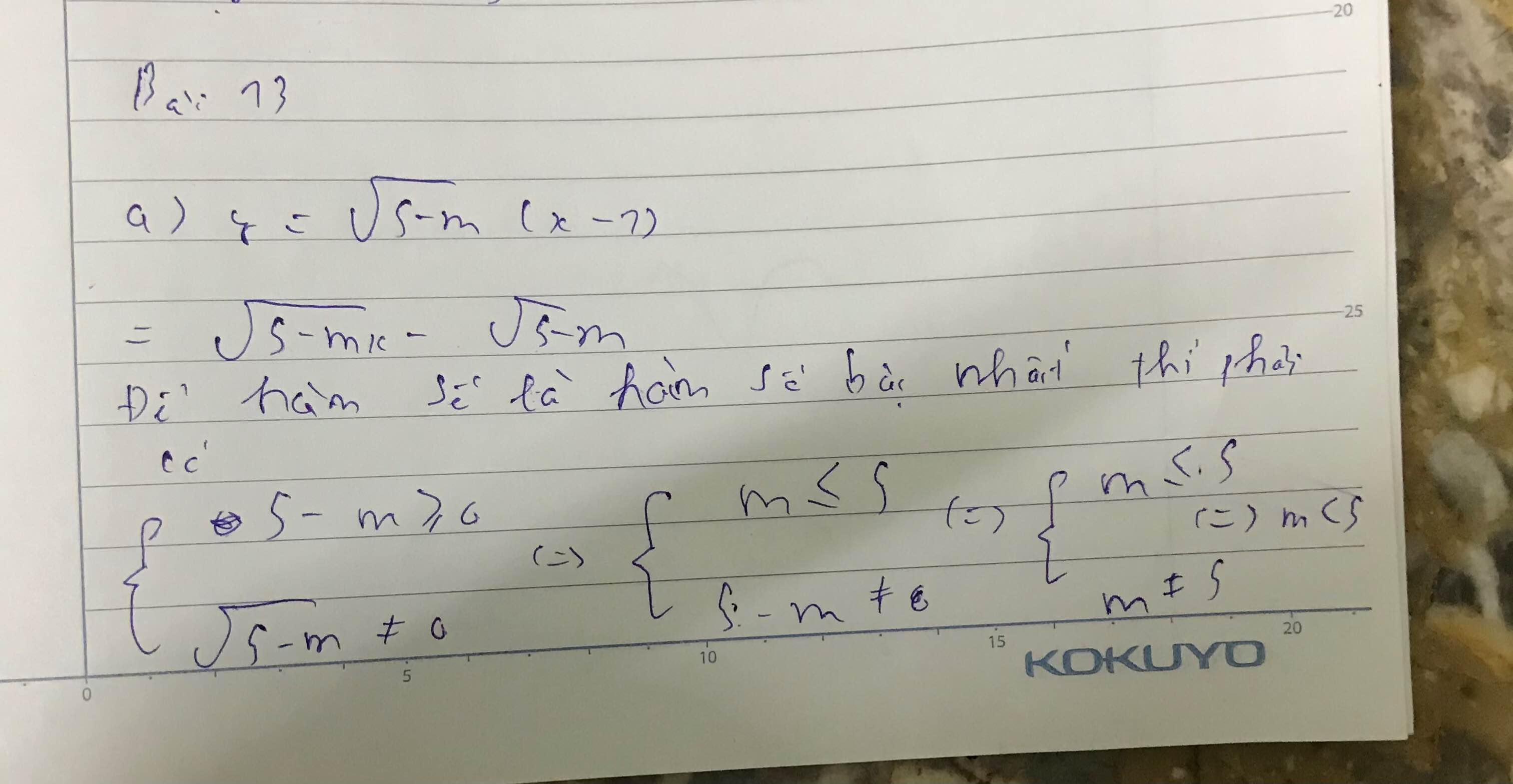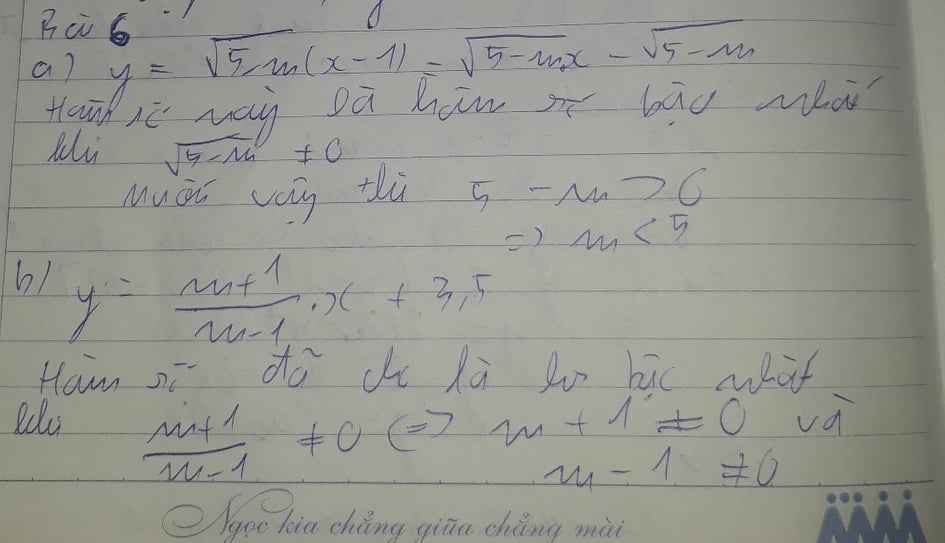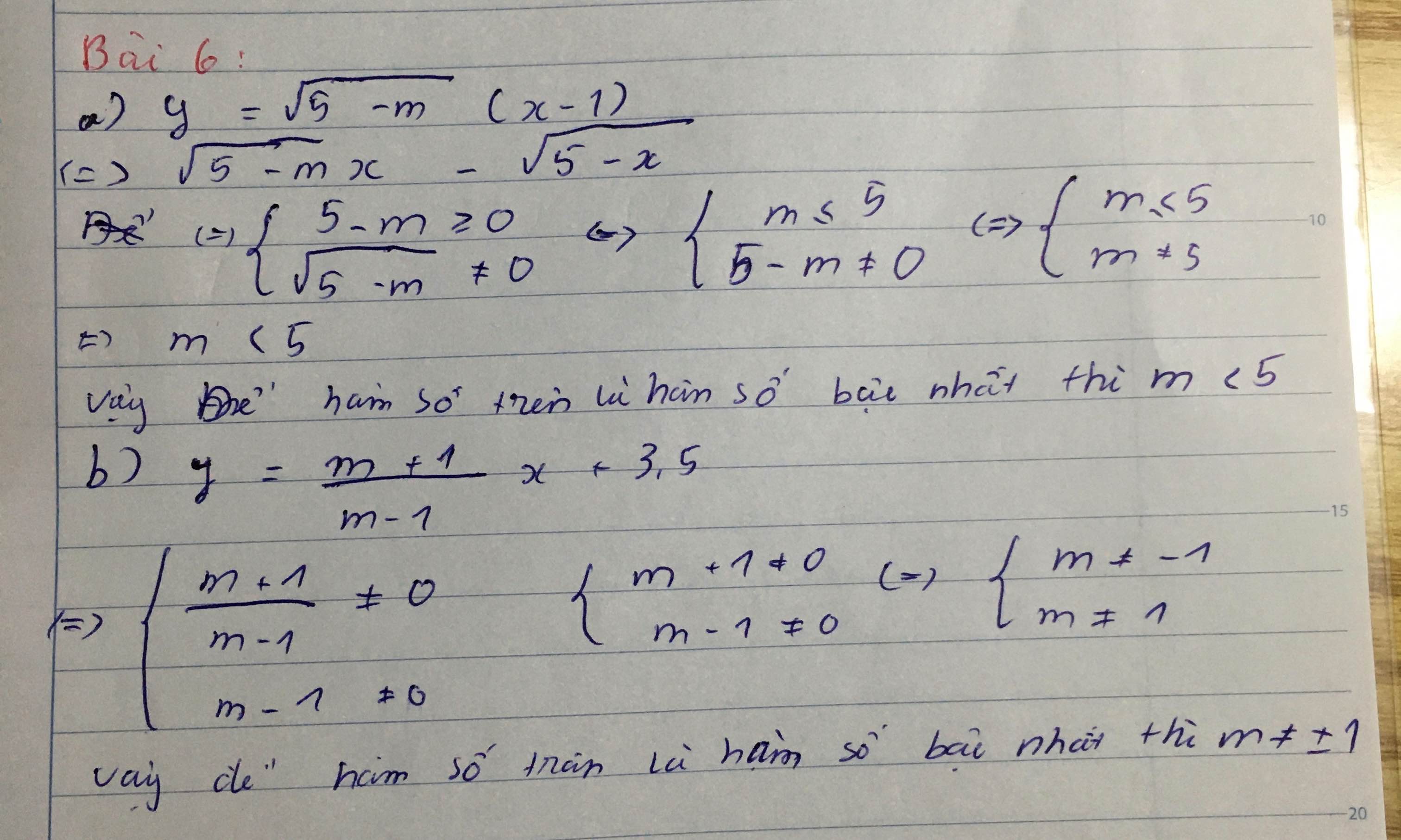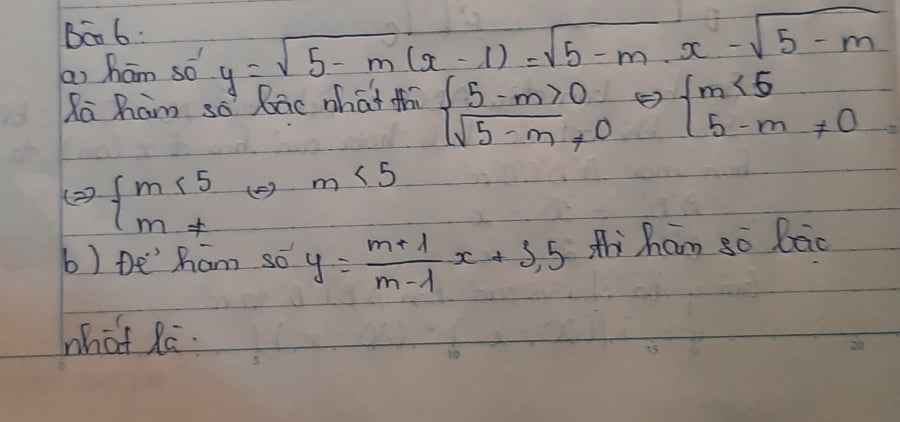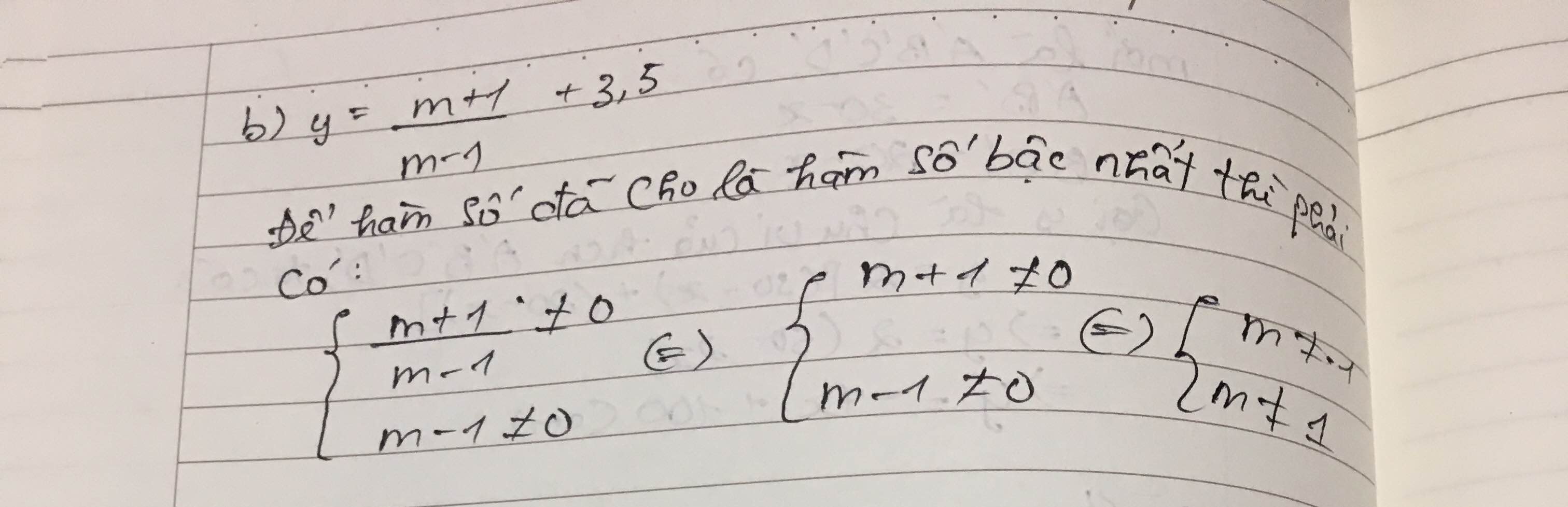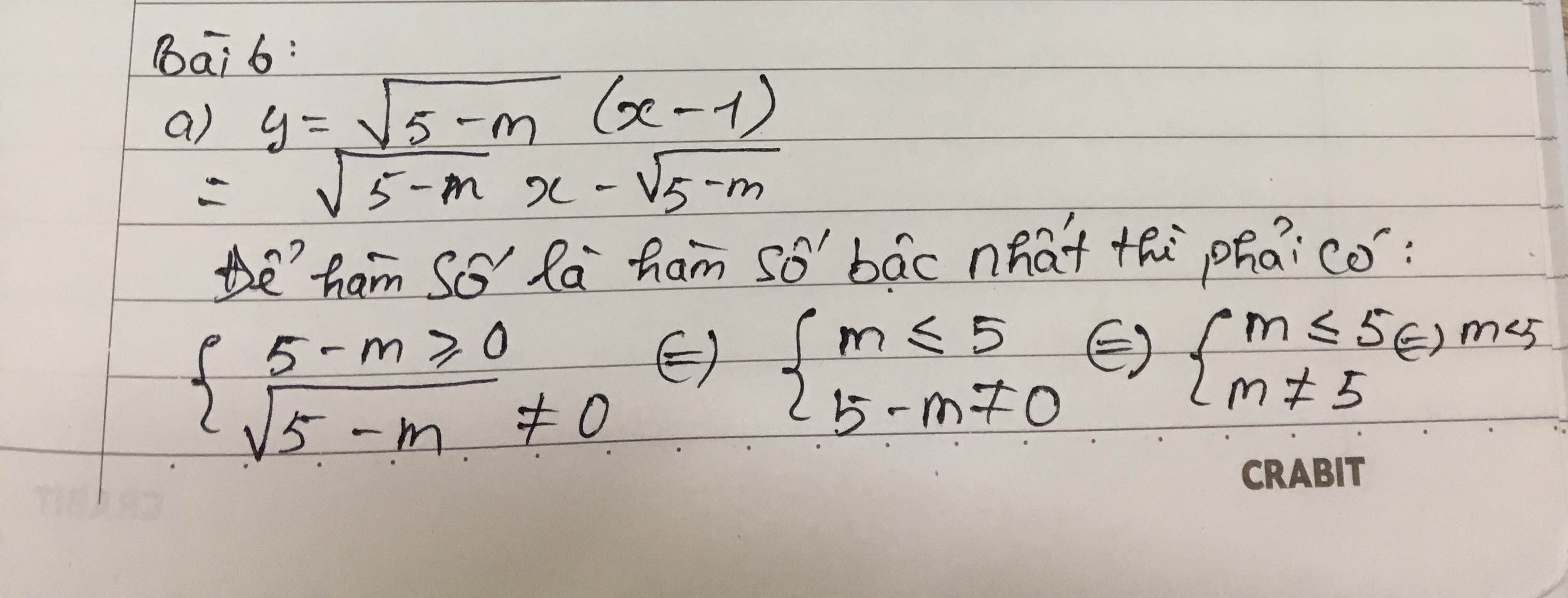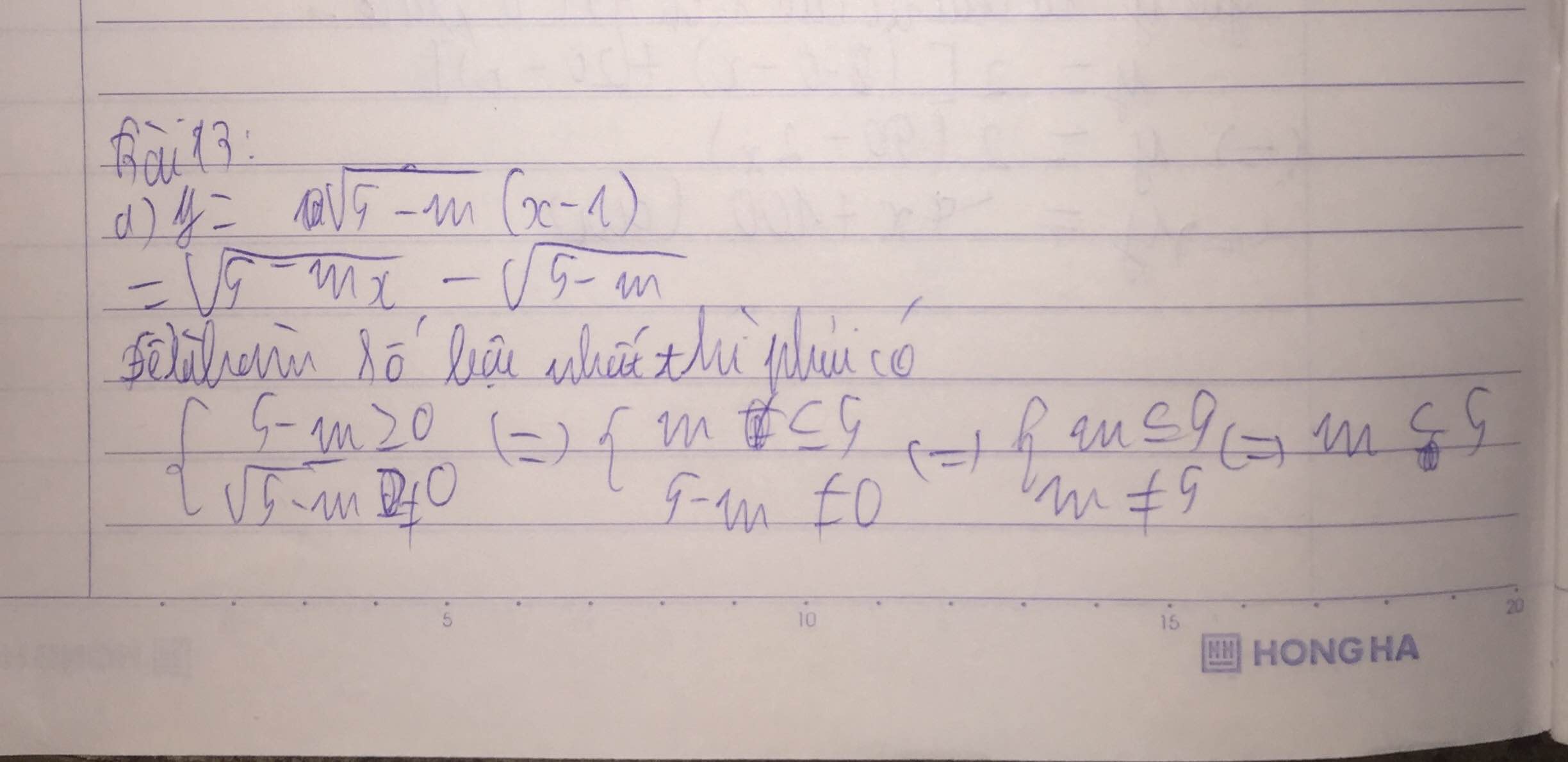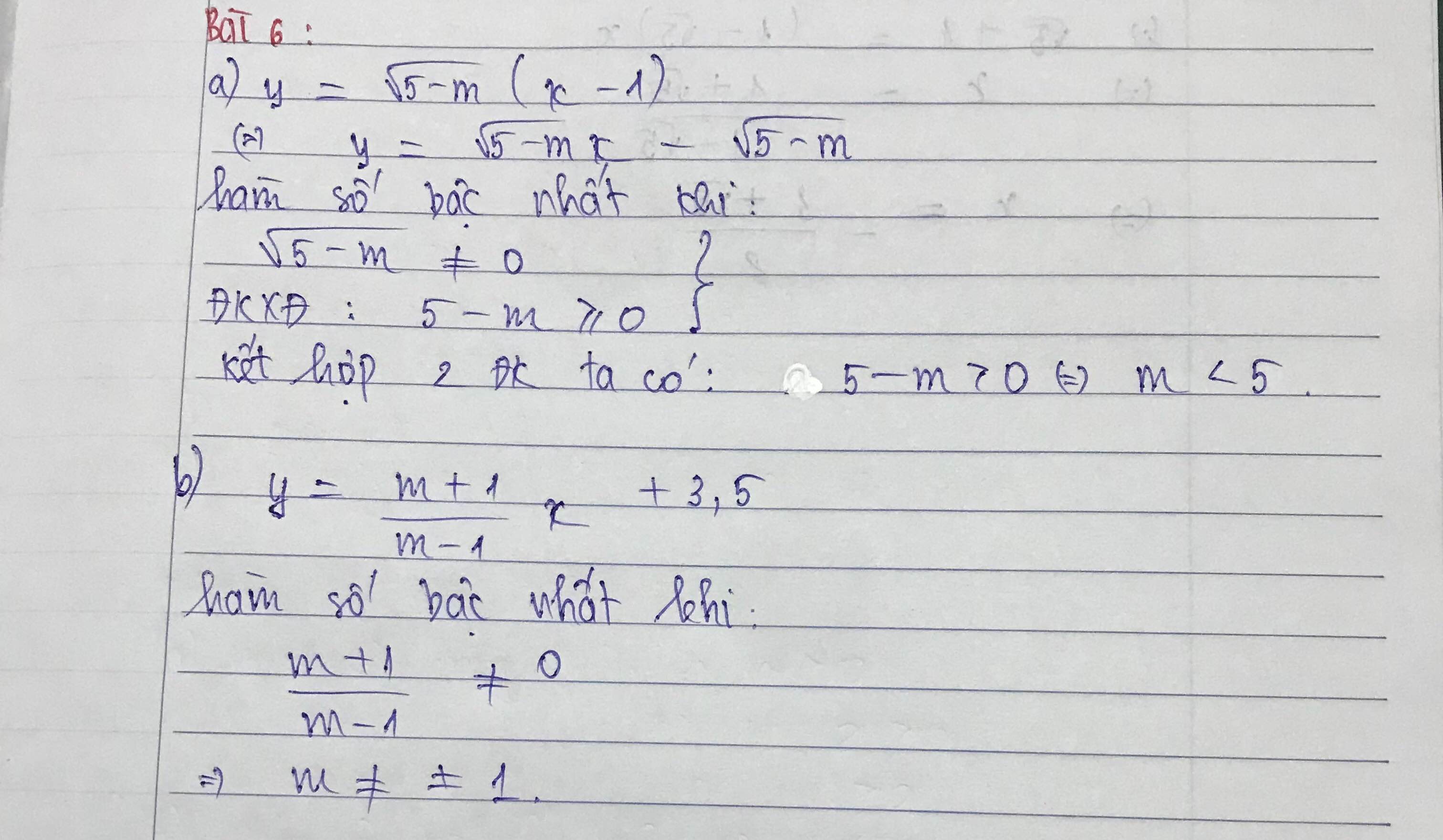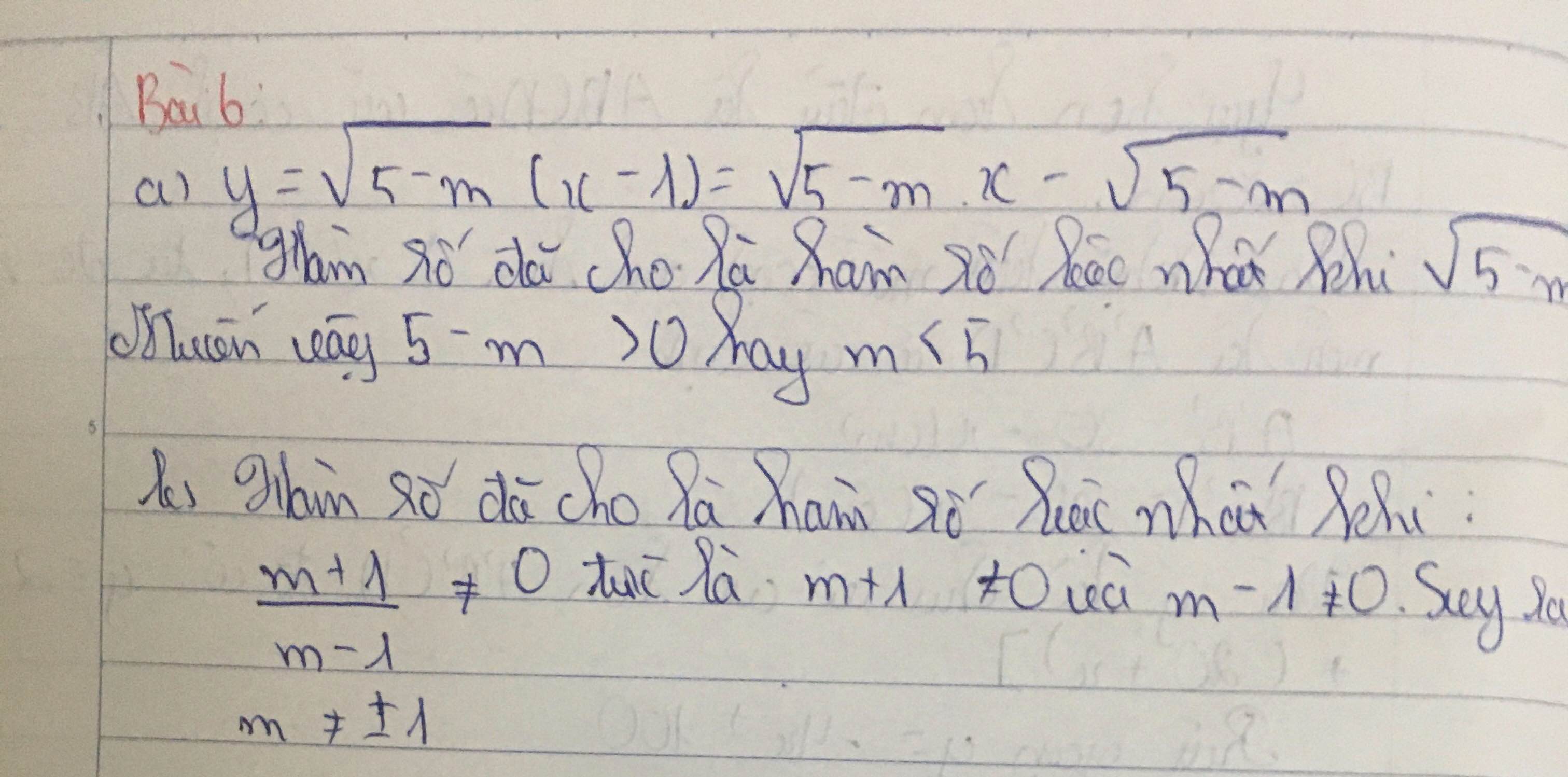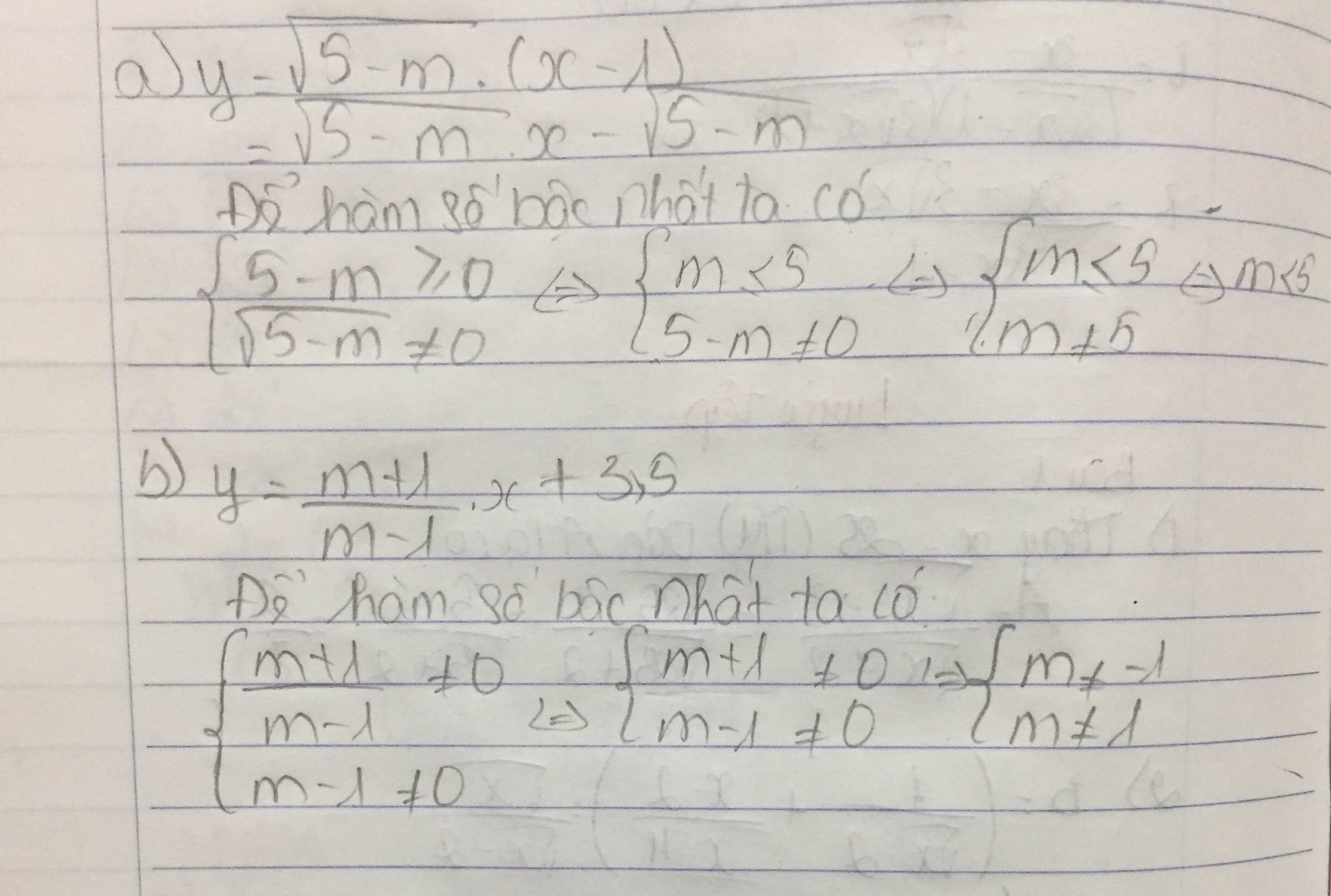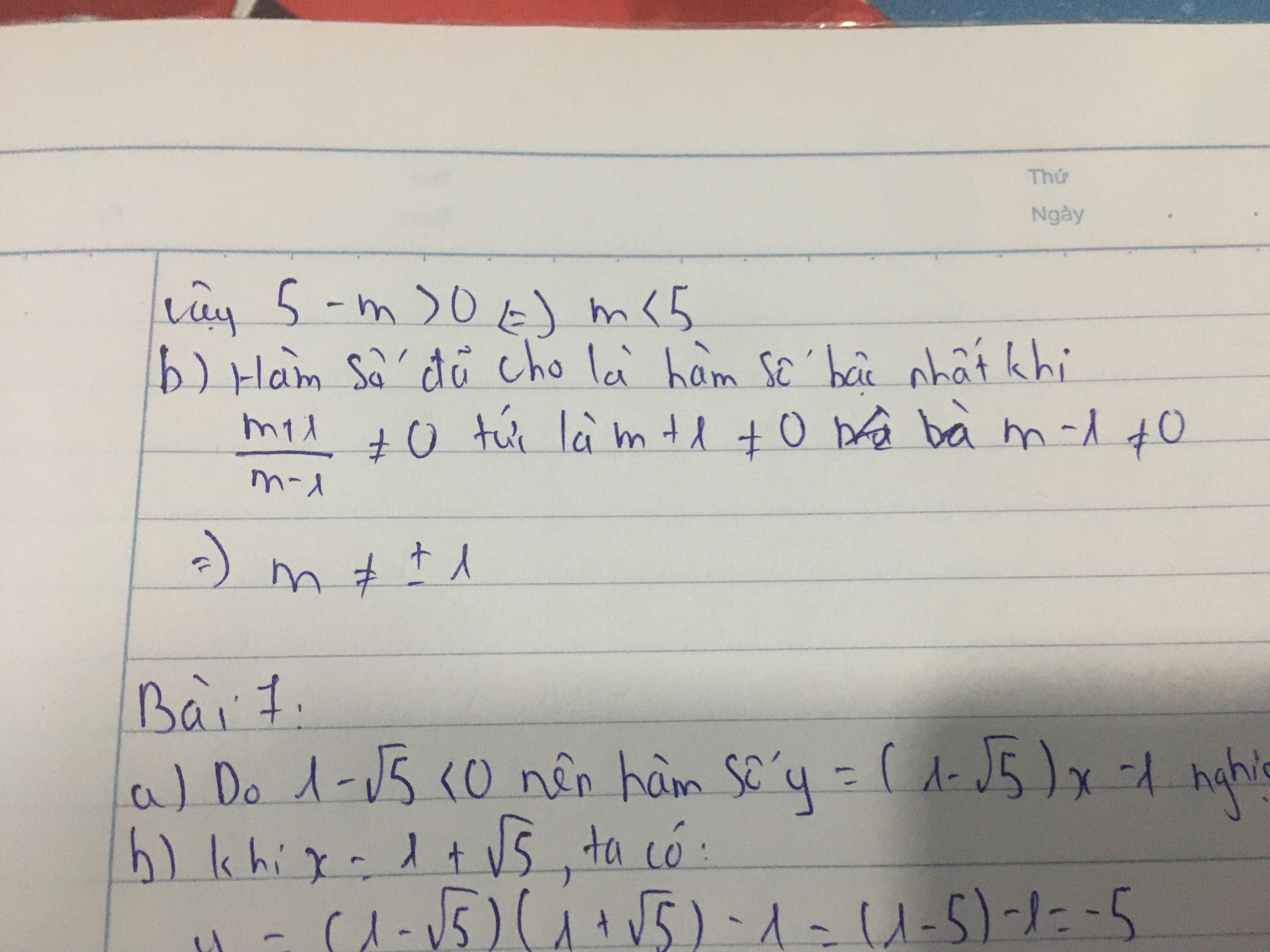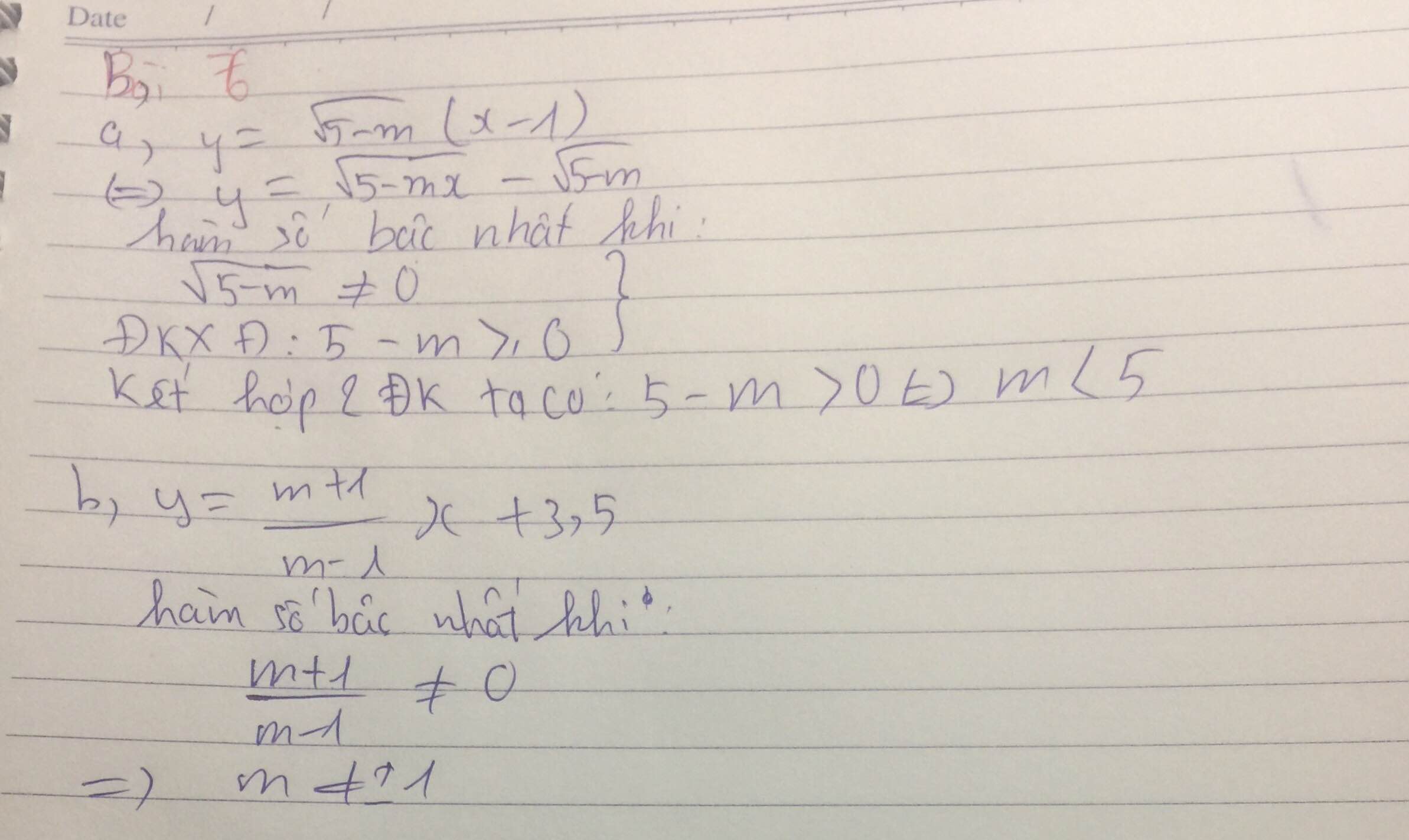a) y=√5−m.(x−1)=√5−m.x−√5−my=5−m.(x−1)=5−m.x−5−m.
Hàm số đã cho là hàm số bậc nhất khi √5−m≠05−m≠0. Muốn vậy 5−m>05−m>0 hay m<5m<5.
b) Hàm số đã cho là hàm số bậc nhất khi
m+1m−1≠0m+1m−1≠0 tức là m+1≠0m+1≠0 và m−1≠0m−1≠0. Suy ra m≠±1m≠±1.
a, \(y=\sqrt{5-m}\left(x-1\right)=\sqrt{5-m}x-\sqrt{5-m}\)
Để hàm số trên là ham số bậc nhất khi
\(\sqrt{5-m}>0\Leftrightarrow5-m>0\Leftrightarrow m< 5\)
b, \(y=\frac{m+1}{m-1}x+3,5\)
Để hàm số trên là hàm số bậc nhất khi \(m-1\ne0\)và \(m+1>0\)
\(\Leftrightarrow m\ne1;m>-1\)
a) \(\sqrt{5-m}\left(x-1\right)=y\) là hàm số bậc nhất thì \(\sqrt{5-m}\ne0\Leftrightarrow5-m\ne0\Leftrightarrow m\ne5\)
b) \(y=\dfrac{m+1}{m-1}x+3,5\) là hàm số bậc nhất thì \(\dfrac{m+1}{m-1}\ne0\Leftrightarrow\left\{{}\begin{matrix}m+1\ne0\\m-1\ne0\end{matrix}\right.\Rightarrow m\ne\pm1\)
a) y = căn (5 - m) .(x - 1) = căn (5 - m).x - căn(5 - m)
Hs đã cho là hsbn khi căn(5 - m) khác 0
hay 5 - m > 0 => m< 5
Vậy ...
b) Hs đã cho là hsbn khi (m + 1) / (m - 1) khác 0
hay m + 1 khác 0 hoặc m - 1 khác 0 => m khác -1 hoặc m khác 1
a\()\)y= \(\sqrt{5-m}.(x-1)=\)\(\sqrt{5-m}.x-\sqrt{5-m}\)
Hàm số đã cho là hàm số bậc nhất khi \(\sqrt{5-m}\ne0\). muốn vậy 5-m >0 hay m<5
b\()\)hàm số đã cho là hàm số bậc nhất khi
\(\dfrac{m+1}{m-1}\ne0\)tức là m+1 \(\ne0\)và m-1 \(\ne\)0. suy ra m\(\ne\)\(\dfrac{+}{ }\)1
a) Ta có
Hệ số là .
Điều kiện để là hàm số hàm bậc nhất là:
Vậy thì hàm số đã cho là hàm số bậc nhất.
Hệ số
a) \(y=\sqrt{5-m}\times\left(x-1\right)=\sqrt{5-m}\times x-\sqrt{5-m}\)
Hàm số đã cho là hàm số bậc nhất khi \(\sqrt{5-m}\ne0\). Muốn vậy \(5-m\) >0 hay \(m\)<5
b) Hàm số đã cho là hàn số bậc nhất khi
\(\dfrac{m+1}{m-1}\ne0\) tức là \(m+1\ne0\) và \(m-1\ne0\) .Suy ra \(m\ne\pm1\)
a) .
Hàm số đã cho là hàm số bậc nhất khi . Muốn vậy hay .
b) Hàm số đã cho là hàm số bậc nhất khi
tức là và . Suy ra .
a) .
Hàm số đã cho là hàm số bậc nhất khi . Muốn vậy hay .
b) Hàm số đã cho là hàm số bậc nhất khi
tức là và . Suy ra .
a) x - \(\sqrt{5-m}\)
Hàm số đã cho là hàm số bậc nhất khi \(\sqrt{5-m}\) ≠ 0. Muốn vậy hay .
b) Hàm số đã cho là hàm số bậc nhất khi
\(\dfrac{m+1}{m-1}\)
≠ tức là ≠ và ≠. Suy ra ≠
a) Ta có :
y = \(\sqrt{5-m}\) ( x - 1) \(\Leftrightarrow\) y = \(\sqrt{5-m}\) .x - \(\sqrt{5-m}\)
\(\Rightarrow\) Hệ số là a = \(\sqrt{5-m}\)
Điều kiện để y = \(\sqrt{5-m}\) . x - \(\sqrt{5-m}\) là hàm số hàm số bậc nhất là :
\(\left\{{}\begin{matrix}\sqrt{5-m}\ne0\\5-m\ge0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}5-m\ne0\\5-m\ge0\end{matrix}\right.\)
\(\Leftrightarrow\) 5 - m > 0 \(\Leftrightarrow\) m < 5
Vậy m < 5 thì hàm số đã cho là hàm số bậc nhất
b) Ta có :
y = \(\dfrac{m+1}{m-1}\)x + 3,5 \(\Rightarrow\) Hệ số a = \(\dfrac{m+1}{m-1}\)
Điều kiện để hàm số y = \(\dfrac{m+1}{m-1}x+3,5\) là hàm bậc nhất là :
\(\left\{{}\begin{matrix}\dfrac{m+1}{m-1}\ne0\\m-1\ne0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m+1\ne0\\m-1\ne0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m\ne-1\\m\ne1\end{matrix}\right.\)
Vậy m \(\ne\) \(\pm1\) thì hàm số đã cho là hàm số bậc nhất
a, Hàm số y = \(\sqrt{5-m}\) (x - 1) là hàm số bậc nhất khi \(\sqrt{5-m}\) ≠ 0
=> \(\sqrt{5-m}\) > 0
<=> 5 - m > 0
<=> - m > -5
<=> m < 5
b, Hàm số y = \(\dfrac{m+1}{m-1}\)x + 3,5 là hàm số bậc nhất khi \(\dfrac{m+1}{m-1}\) ≠ 0
=> \(\left\{{}\begin{matrix}m+1\ne0\\m-1\ne0\end{matrix}\right.\)
<=> \(\left\{{}\begin{matrix}m\ne-1\\m\ne1\end{matrix}\right.\)
<=> m ≠ \(\pm1\)
a)\(y=\sqrt{5-m}\left(x-1\right)=\sqrt{5-m}.x-\sqrt{5-m}\)
Hàm số đã cho là hàm số bậc nhất khi \(\sqrt{5-m}\) ≠ 0.Muốn vậy 5-m>0 hay m<0
b)Hàm số đã cho là hàm số bậc nhất khi:
\(\dfrac{m+1}{m-1}\)≠0 tức là m+1≠0 và m-1≠0 ⇒m≠-1;m≠1