Question

Bài 1: Cho hình thang cân ABCD có AB//CD, đường chéo DB vuông góc với cạnh bên BC, DB là tia phân giác góc D. Tính chu vi của hình thang, biết BC=3cm.

Bài 2: Cho tam giác ABC cân tại A, các đường phân giác BD,CE (D thuộc AC, E thuộc AB)

                  a) Chứng minh BEDC là hình thang cân

                  b) Tính các góc của hình thang cân BEDC, biết góc C=50 độ

Bài 3: Cho hình thang cân ABCD có AB//CD, O là giao điểm của hai đường chéo, E là giao điểm của hai đường thẳng chứa cạnh bên AD và BC. Chứng minh:

                a) OA=OB , OC=OD

                b) EO là đường trung trực của hai đáy hình thang ABCD. 

            Các bạn giải giúp mình bài này nhé. Cảm ơn các bạn.

Answer 1

Bài 2:

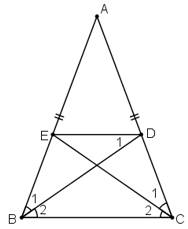
Ta có: ∆ABC là ∆ cân tại A(gt)

=>∠ABC=∠ACB

+Ta có BD là tia pgiac của ∠ABC

=>∠B₁=∠B₂=1/2∠ABC

+Ta có CE là tia pgiac ∠ACB

=>C₁=C₂=1/2∠ACB

Xét ∆

AEC và ΔADB có:

+∠A chung

+AB=AC

+C₁=B₁

=> ΔAEC = ΔADB

=> AE = AD

=>BCDE là hình thang cân

b) Ta có ∠ACB=∠ABC=50^o(do BCDE là hình thang cân)

Ta có: ED//BC

\(\Rightarrow\left\{{}\begin{matrix}\widehat{ABC}=\widehat{AED}\\\widehat{ACB}=\widehat{ADE}\end{matrix}\right.=50^o}\) (SLT)

Mà ∠DEB=∠EDC

Ta có:

+∠DEB+∠AED=180^o (kề bù)

=>50^o+∠AED=180^o

=>∠AED=180^o-50^o=130^o

=>∠AED=∠ADE=130^o

Answer 2

Bài 1:

 

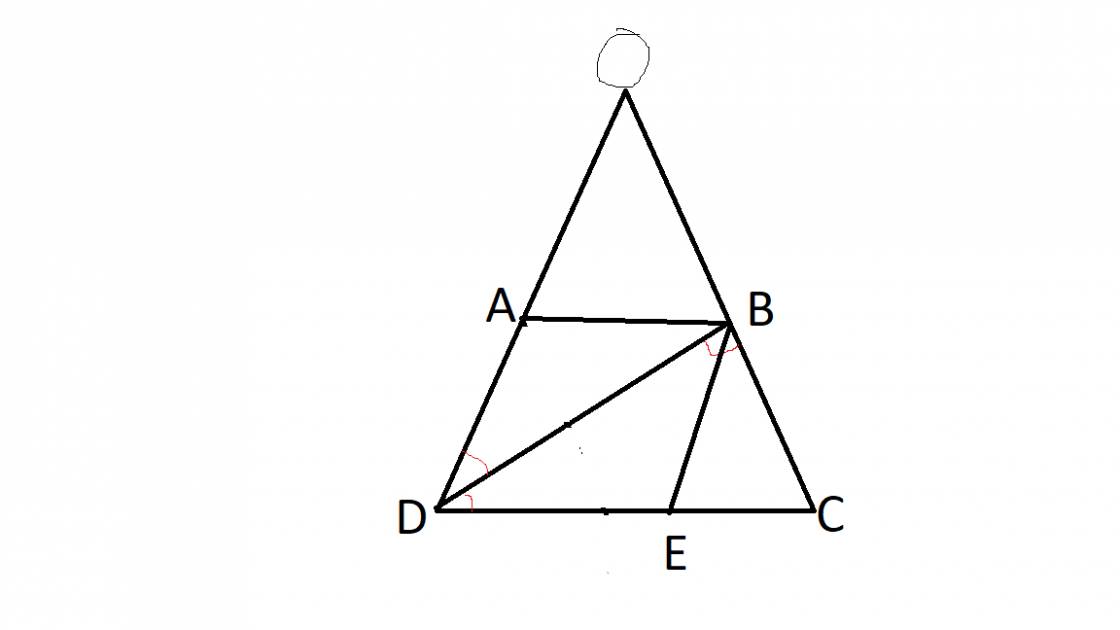
Ta có: AD=BC=3cm (t/c hthang)

Vì AB//CD(gt) nên \(\widehat{ABD}=\widehat{BDC}\left(SLT\right)\)

Mà \(\widehat{ADC}=\widehat{BDC}\) (do BD là tia pgiac góc D)

=>∠ABD=∠BDC 

=>∆ABD cân tại A

=>AD=BC=3cm

Vì ∆DBC vuông tại B

nên ∠BDC+∠C=90^o

Mà ∠ADC=∠C (do ABCD là hình thang cân)

và ∠BDC=1/2 ∠ADC

=> ∠BCD=1/2∠C

Khi đó: ∠C+1/2∠C=90^o=>∠C=60^o

- Kẻ từ B 1 đường thẳng // AD cắt CD tại E

Hình thang ABED có hai cạnh bên song song nên AB = DE và AD = BE

⇒ DE = 3 (cm), BE = 3 (cm)

Mà ∠BEC=∠ADC(đồng vị)

=>∠BEC=∠C

=>∆BEC cân tại B có ∠C=60^o

=>∆BEC là ∆ cả cân cả đều

=> EC=BC=3cm

Ta có: CD = CE + ED = 3 + 3 = 6(cm)

Chu vi hình thang ABCD bằng:

AB + BC + CD + DA = 3 + 3 + 6 + 3 = 15 (cm)

Answer 3

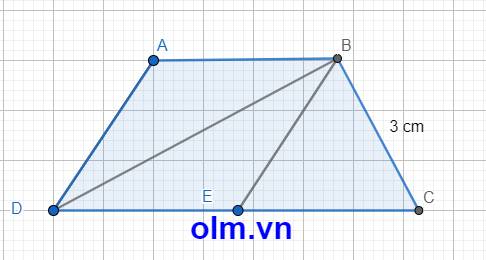
Xét \(\Delta\)ABD có: \(\widehat{ABD}\) = \(\widehat{BDC}\) ( hai góc so le trong)

                         \(\widehat{ADB}\) = \(\widehat{BDC}\) (BD là phân giác của góc \(\widehat{ABD}\))

            ⇒          \(\widehat{ABD}\) =  \(\widehat{ADB}\) (vì cùng bằng góc BDC)

             ⇒          \(\Delta\) ABD cân tại A ⇒ AB = AD = 3 cm

Gọi E là trung điểm của DC ta có:\(\Delta\)BCD vuông tại B nên

BE = DE = EC (trong tam giác vuông trung tuyến ứng với cạnh huyền bằng \(\dfrac{1}{2}\) cạnh huyền)

Mặt khác ta có: \(\widehat{ADC}\) = \(\widehat{DCB}\) ( vì ABCD là hình thang cân)

⇒\(\widehat{BDC}\) = \(\dfrac{1}{2}\) \(\widehat{DCB}\) ⇒ \(\widehat{DCB}\) + \(\dfrac{1}{2}\)\(\widehat{DCB}\) = 90⁰ 

⇒ \(\widehat{DCB}\) \(\times\) ( 1 + \(\dfrac{1}{2}\)) = 90⁰

⇒ \(\widehat{DCB}\) = 90⁰ : \(\dfrac{3}{2}\) = 60⁰ 

Xét \(\Delta\)BCE có BE = EC và  \(\widehat{BCE}\) = 60⁰ nên \(\Delta\)BCE là tam giác đều

⇒ BE = EC = BC = 3 cm 

⇒ DC = BE \(\times\) 2 = 3 \(\times\) 2 = 6 cm

Chu vi của hình thang ABCD là:

3 + 3 + 6 + 3 = 15 (cm)

Kết luận chu vi hình thang là: 15 cm