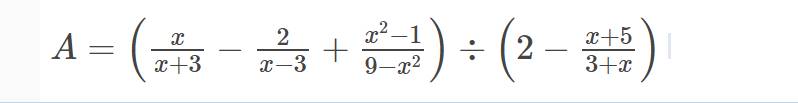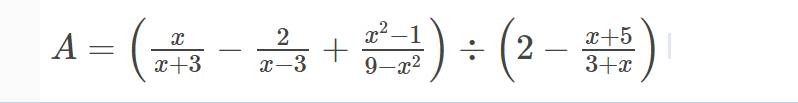Question

Bài 1 2(x^2+y^2) = (x-y)^2

Bài 2

Cho a>b>c và a-b=7 ab=60. Không tính a,b tính a^2-b^2,a^4+6^4

Bạn naò biết dungf HĐT phụ giúp mình với nhé

 

Answer 1

\(\left(a-b\right)^2=a^2+b^2-2ab\\ \Rightarrow49=a^2+b^2-120\Rightarrow a^2+b^2=169\)

\(\left(a+b\right)^2=a^2+b^2+2ab=169+120=289\\ \Rightarrow a+b=17\)

\(a^2-b^2=\left(a-b\right)\left(a+b\right)=7\cdot17=119\)

\(a^4+b^4=\left(a^2+b^2\right)^2-2a^2b^2=169^2-2\cdot60^2\\ =28561-7200=21361\)

Answer 2

\(2\left(x^2+y^2\right)=\left(x-y\right)^2\\ \Rightarrow2x^2+2y^2=x^2-2xy+y^2\\ \Rightarrow x^2+2xy+y^2=0\\ \Rightarrow\left(x+y\right)^2=0\Rightarrow x+y=0\Rightarrow x=-y\)