= \(\infty\)
@Cua
#kalac
= \(\infty\)
@Cua
#kalac
Tính bằng cách thuận tiện nhất a 4,8 x 0,25 x 0,4 x 0,02b 12,5 x 15,32 x 0,008 15,32 x 0,9
84000 : 125 : 8 tính bằng cách thuận tiện nhất
Tính bằng cách thuận tiện nhất:
A = 1 giờ 24 phút + 1,4 giờ x 7 + 2 giờ 10 phút + 38 phút=.......
Tính tích phân I = ∫ 0 1 2 4 − x 2 d x bằng cách đặt x=2sint. Mệnh đề nào dưới đây đúng?
A. I = 2 ∫ 0 1 d t
B. I = 2 ∫ 0 π 6 d t
C. I = ∫ 0 π 3 d t
D. I = ∫ 0 π 6 d t
Tính tích phân I=\(\int\limits^{\pi}_0\)\(x^2cos2xdx\) bằng cách đặt \(\left\{{}\begin{matrix}u=x^2\\dv=cos2xdx\end{matrix}\right.\).Mệnh đề nào dưới đây đúng?
A. \(I=\dfrac{1}{2}x^2sin2x|^{^{\pi}_0}-\int\limits^{\pi}_0xsin2xdx\)
B. \(I=\dfrac{1}{2}x^2sin2x|^{^{\pi}_0}-2\int\limits^{\pi}_0xsin2xdx\)
C. \(I=\dfrac{1}{2}x^2sin2x|^{^{\pi}_0}+\int\limits^{\pi}_0xsin2xdx\)
D. \(I=\dfrac{1}{2}x^2sin2x|^{^{\pi}_0}+2\int\limits^{\pi}_0xsin2xdx\)
Gọi ∆ là tiếp tuyến tại điểm M( x 0 ; y 0 ), x 0 < 0 thuộc đồ thị hàm số y = x + 2 x + 1 sao cho khoảng cách từ I(-1;1) đến ∆ đạt giá trị lớn nhất, khi đó x0, y0 bằng
A. -2.
B. 2.
C. -1.
D. 0.
Trong không gian Oxyz, cho mặt cầu (S): ( x + 1 ) 2 + ( y - 1 ) 2 + ( z - 2 ) 2 = 9 và mặt phẳng (P): 2x-2y+z+14=0. Gọi M ( a ; b ; c ) là điểm thuộc mặt cầu (S) sao cho khoảng cách từ M đến mặt phẳng (P) lớn nhất. Tính T = a + b + c .
![]()
![]()
![]()
![]()
Tính nguyên hàm I = ∫ d x x x 2 + 4 bằng cách đặt t = x 2 + 4 , mệnh đề nào dưới đây đúng?
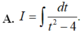
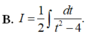
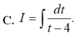
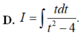
Tính nguyên hàm I = ∫ d x x x 2 + 4 bằng cách đặt t = x 2 + 4 , mệnh đề nào dưới đây đúng?
A. I = ∫ d t t 2 − 4 .
B. I = 1 2 ∫ d t t 2 − 4 .
C. I = ∫ d t t − 4 .
D. I = ∫ t d t t 2 − 4 .