\(B=\left(1-\frac{2}{5}\right)\left(1-\frac{2}{7}\right)\left(1-\frac{2}{9}\right)....\left(1-\frac{2}{99}\right)\)
\(B=\frac{3}{5}\cdot\frac{5}{7}\cdot\frac{7}{9}\cdot...\cdot\frac{97}{99}\)
\(B=\frac{3\cdot5\cdot7\cdot...\cdot97}{5\cdot7\cdot9\cdot...\cdot99}=\frac{3}{99}=\frac{1}{33}\)
Vậy B = \(\frac{1}{33}\)
\(\left[1-\frac{2}{5}\right]\left[1-\frac{2}{7}\right]\left[1-\frac{2}{9}\right]...\left[1-\frac{2}{99}\right]\)
\(=\frac{3}{5}\cdot\frac{5}{7}\cdot\frac{7}{9}\cdot...\cdot\frac{97}{99}\)
\(=\frac{3\cdot5\cdot7\cdot...\cdot97}{5\cdot7\cdot9\cdot...\cdot99}=\frac{3}{99}=\frac{1}{33}\)
\(\frac{1-2}{5}\times\frac{1-2}{7}\times\frac{1-2}{9}\times...\times\frac{1-2}{99}\)
\(=\frac{3}{5}\times\frac{5}{7}\times\frac{7}{9}\times...\times\frac{97}{99}\)
\(=\frac{3}{99}\)
\(=\frac{1}{33}\)
mình chỉ ghi lời giải thôi không ghi đề nhé
B = 3/5*5/7*7/9*..........*97/99
B=3/99=1/33
\(B=\left(1-\frac{2}{5}\right).\left(1-\frac{2}{7}\right).\left(1-\frac{2}{9}\right).....\left(1-\frac{2}{99}\right)\)
\(B=\frac{3}{5}.\frac{5}{7}.\frac{7}{9}.....\frac{97}{99}\)
\(B=\frac{3.5.7.....97}{5.7.9.....99}\)
\(B=\frac{3}{99}\)
\(B=\frac{1}{33}\)
Vậy B = 1/33















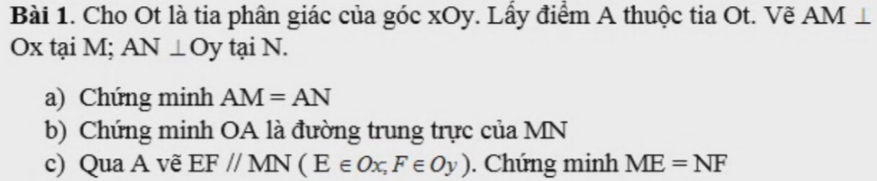 câu C thôi nhé. Nhanh hộ mìn
câu C thôi nhé. Nhanh hộ mìn