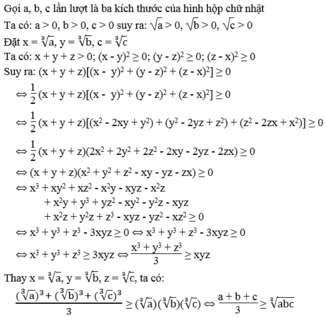
Vì a + b + c 3 ≥ a b c 3 và a + b + c 3 không đổi nên a + b + c 3 đạt giá trị nhỏ nhất ∛abc khi a = b = c.
Vậy trong các hình hộp chữ nhật có cùng thể tích thì hình lập phương có tổng ba kích thước bé nhất.
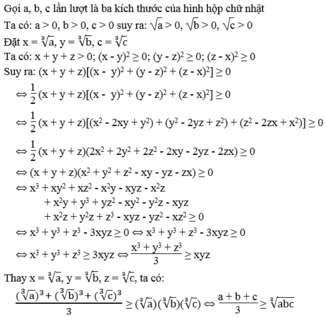
Vì a + b + c 3 ≥ a b c 3 và a + b + c 3 không đổi nên a + b + c 3 đạt giá trị nhỏ nhất ∛abc khi a = b = c.
Vậy trong các hình hộp chữ nhật có cùng thể tích thì hình lập phương có tổng ba kích thước bé nhất.
Áp dụng bất đẳng thức Cô-si cho ba số không âm, chứng minh: Trong các hình hộp chữ nhật có cùng tổng ba kích thước thì hình lập phương có thể tích lớn nhất.
Áp dụng bất đẳng thức Cô-si cho hai số không âm, chứng minh: Trong các hình chữ nhật có cùng diện tích thì hình vuông có chu vi bé nhất.
Áp dụng bất đẳng thức Cô - si cho hai số không âm, chứng minh :
a) Trong các hình chữ nhật có cùng chu vi thì hình vuông có diện tích lớn nhất
b) Trong các hình chữ nhật có cùng diện tích thì hình vuông có chu vi bé nhất
Áp dụng bất đẳng thức Cô-si cho hai số không âm, chứng minh: Trong các hình chữ nhật có cùng chu vi thì hình vuông có diện tích lớn nhất.
Áp dụng bđt cosi cho các số ko âm cmr :
a, Trong các hinh hộp chữ nhật có cùng tổng 3 kích thước thì hình lập phương có thể tích lớn nhất
b, Trong các hình hộp chữ nhật có cùng thể tích thì hình lập phương có tổng 3 kích thước nhỏ nhất
Ai làm đúng và nhanh nhất mk tk cho
Đố các bạn: (chắc cũng dễ)
a) Chứng minh: Trong tất cả các hình hộp chữ nhật có cùng tổng 3 kích thước, hình lập phương có thể tích lớn nhất và trong tất cả các hình hộp chữ nhật có cùng thể tích thì hình lập phương có tổng 3 kích thước nhỏ nhất.
b) Một chai nước hình nón chứa một lượng nước bên trong sao cho mặt nước cách đỉnh chai 8cm. Nếu lật ngược chai lại thì lúc này mặt nước cách đáy chai 2cm. Tính chiều cao của chai nước đó.
Áp dụng BĐT Cô-si CMR:
a, Trong các hình chữ nhật có cùng chu vi thì hình vuông có diện tích lớn nhất
b, Trong các hình chữ nhật có cùng diện tích thì hình vuông có chu vi nhỏ nhất
Chứng minh: x 3 + y 3 + z 3 - 3 x y z = 1 / 2 . x + y + z x - y 2 + y - z 2 + z - x 2
Từ đó chứng tỏ: Với ba số a, b, c không âm thì x 3 + y 3 + z 3 3 ≥ x y z
(Bất đẳng thức Cô-si cho ba số không âm)
Dấu đẳng thức xảy ra khi ba số a, b, c bằng nhau.
Một hình chữ nhật có 3 kích thước \(x;y;z\left(x;y;z>0\right)\)có độ dài đường chéo lớn là \(\sqrt{2}\). Nếu xếp 3 kích thước đó lại thành một đoạn thẳng thì đoạn thẳng này sẽ có độ dài bằng 1. Nếu ta lập 3 khối lập phương có cạnh lần lượt là 3 kích thước của hình hộp chữ nhật đã cho thì tổng thể tích của 3 khối lập phương mới này bằng 3. Tính giá trị của biểu thức \(P=x^5+y^5+z^5\)