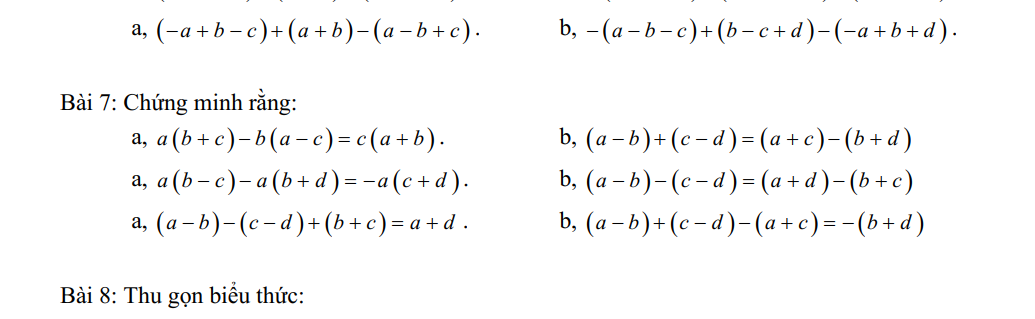Question

anh chị bạn bè nào còn thức giúp

Answer 1

a) a(b + c) - b(a - c)

= ab + ac - ab + bc

= c(a + b)

b) (a - b) + (c - d)

= a - b + c - d

= (a + c) - (b + d)

 

Answer 2

Lời giải:

a.

$a(b+c)-b(a-c)=(ab+ac)-(ab-bc)=ab+ac-ab+bc=ac+bc=c(a+b)$

b.

$a(b-c)-a(b+d)=(ab-ac)-(ab+ad)=ab-ac-ab-ad=-ac-ad$

$=-a(c+d)$

c.

$(a-b)-(c-d)+(b+c)=a-b-c+d+b+c=a+d$

d.

$(a-b)+(c-d)=a-b+c-d=(a+c)-(b+d)$

e.

$(a-b)-(c-d)=a-b-c+d=(a+d)-(b+c)$

f.

$(a-b)+(c-d)-(a+c)=a-b+c-d-a-c=(a-a)+(c-c)-b-d=-(b+d)$