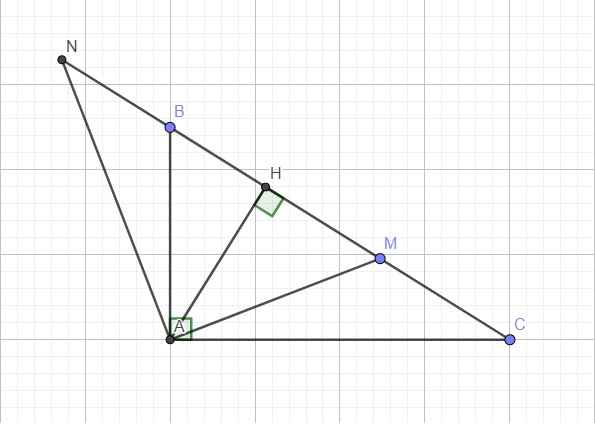
Kẻ đường cao AH ứng với BC \(\Rightarrow\) AH đồng thời là đường cao ứng với cạnh huyền của 2 tam giác vuông ABC và AMN
Trong tam giác vuông ABC, áp dụng hệ thức lượng:
\(\dfrac{1}{AH^2}=\dfrac{1}{AB^2}+\dfrac{1}{AC^2}\)
Trong tam giác vuông ANM:
\(\dfrac{1}{AH^2}=\dfrac{1}{AM^2}+\dfrac{1}{AN^2}\)
\(\Rightarrow\dfrac{1}{AM^2}+\dfrac{1}{AN^2}=\dfrac{1}{AB^2}+\dfrac{1}{AC^2}\) cố định (đpcm)
b.
Ta có:
\(\dfrac{1}{AM^2}+\dfrac{1}{AN^2}=\dfrac{1}{AB^2}+\dfrac{1}{AC^2}=\dfrac{1}{3^2}+\dfrac{1}{4^2}=\dfrac{25}{144}\)
\(\Leftrightarrow\dfrac{25}{144}=\dfrac{1}{AM^2}+\dfrac{1}{AN^2}\ge2\sqrt{\dfrac{1}{AM^2.AN^2}}=\dfrac{2}{AM.AN}\)
\(\Rightarrow AM.AN\ge\dfrac{288}{25}\)
\(\Rightarrow S_{AMN}=2AM.AN\ge\dfrac{576}{25}\left(cm^2\right)\)
Dấu "=" xảy ra khi \(AM=AN\) hay tam giác AMN vuông cân