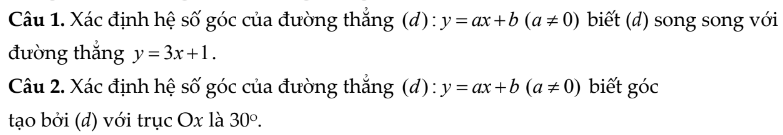a.
\(=\sqrt{\left(2x^2\right)^2}.\sqrt{\left(y-2\right)^2}=2x^2.\left(2-y\right)\)
b.
\(=\dfrac{\sqrt{x+3}-1}{x+3-1}=\dfrac{\left(\sqrt{x+3}-1\right)\left(\sqrt{x+3}+1\right)}{\left(x+3-1\right)\left(\sqrt{x+3}+1\right)}=\dfrac{1}{\sqrt{x+3}+1}\)
c.
\(=\dfrac{\sqrt{x}\left(1+\sqrt{xy}\right)-\sqrt{y}\left(1+\sqrt{xy}\right)}{xy-1}=\dfrac{\left(\sqrt{x}-\sqrt{y}\right)\left(1+\sqrt{xy}\right)}{\left(\sqrt{xy}-1\right)\left(\sqrt{xy}+1\right)}=\dfrac{\sqrt{x}-\sqrt{y}}{\sqrt{xy}-1}\)
d.
\(=\dfrac{x-\sqrt{5}}{x\left(x+\sqrt{2}\right)-\sqrt{5}\left(x+\sqrt{2}\right)}=\dfrac{x-\sqrt{5}}{\left(x+\sqrt{2}\right)\left(x-\sqrt{5}\right)}=\dfrac{1}{x+\sqrt{2}}\)

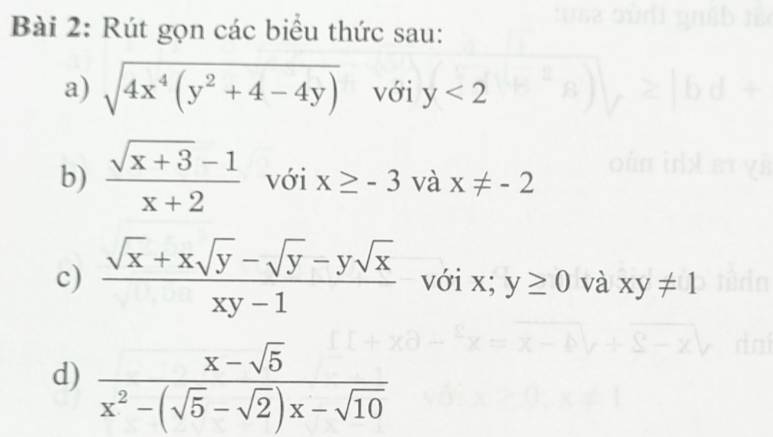 ai giúp mình được không ạ
ai giúp mình được không ạ


 ai giúp mình được không ạ
ai giúp mình được không ạ
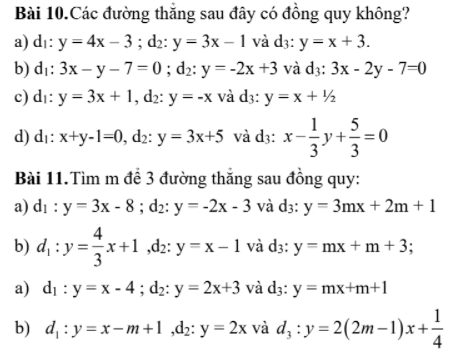
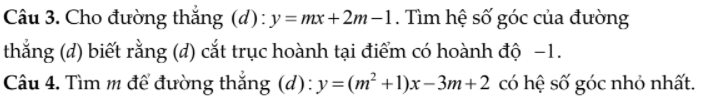 này được
này được 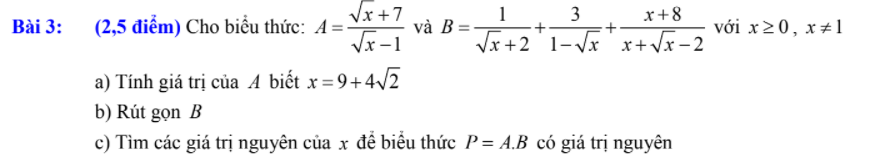 được không ạ, mai em phải nộp rồi, cảm ơn mn nhiều.
được không ạ, mai em phải nộp rồi, cảm ơn mn nhiều.