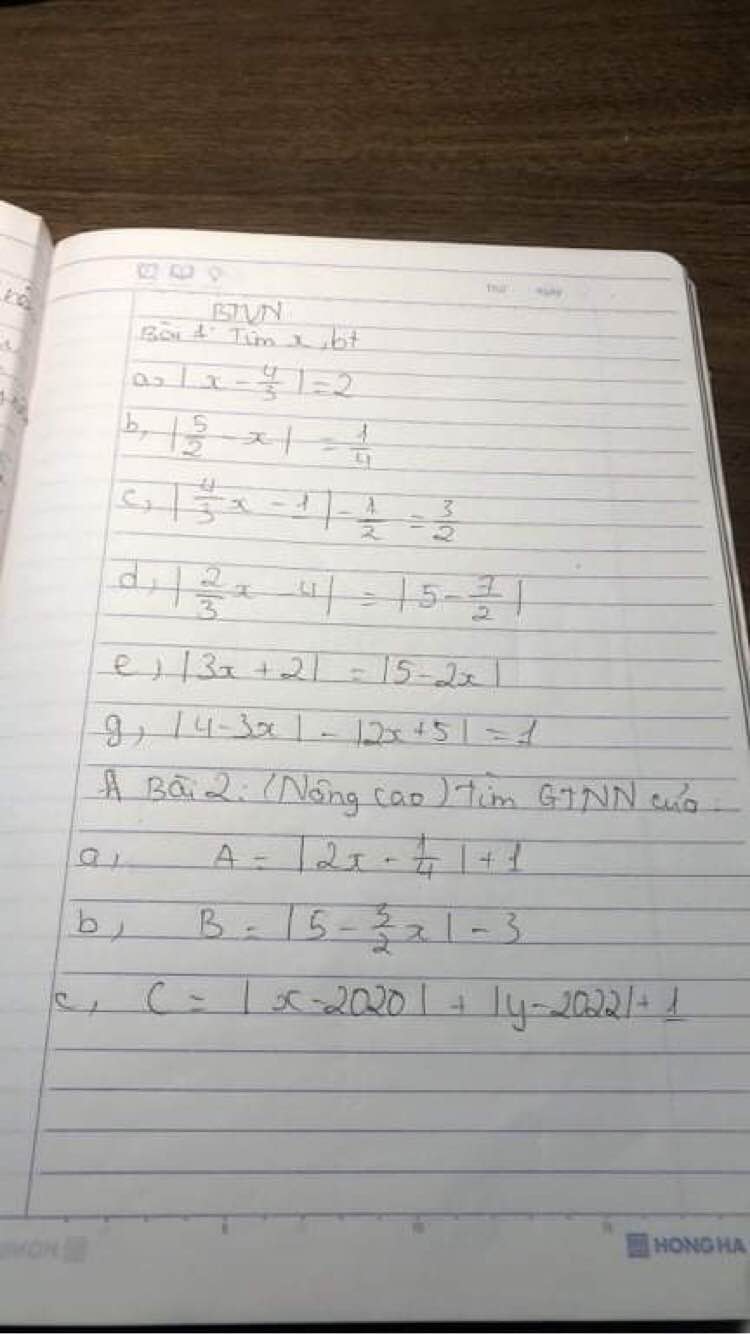Bài 2:
a. $x^2=12y^2+1$ lẻ nên $x$ lẻ
Ta biết một scp khi chia 8 dư $0,1,4$. Mà $x$ lẻ nên $x^2$ chia $8$ dư $1$
$\Rightarrow 12y^2+1\equiv 1\pmod 8$
$\Rightarrow 12y^2\equiv 0\pmod 8$
$\Rightarrow y^2\equiv 0\pmod 2$
$\Rightarrow y$ chẵn. Mà $y$ nguyên tố nên $y=2$.
Khi đó: $x^2=12y^2+1=12.2^2+1=49\Rightarrow x=7$ (tm)
Bài 2:
b.
$x^2=8y+1$ nên $x$ lẻ. Đặt $x=2k+1$ với $k$ tự nhiên.
Khi đó: $8y+1=x^2=(2k+1)^2=4k^2+4k+1$
$\Rightarrow 2y=k(k+1)$
Vì $(k,k+1)=1, k< k+1$ và $y$ nguyên tố nên xảy ra các TH sau:
TH1: $k=2, k+1=y\Rightarrow y=3\Rightarrow x=5$ (tm)
TH2: $k=1, k+1=2y\Rightarrow y=1$ (vô lý)
TH3: $k=y, k+1=2\Rightarrow y=1$ (vô lý)
Vậy $(x,y)=(5,3)$ là đáp án duy nhất thỏa mãn.
Bài 3:
a. $A=\frac{5-x}{x+2}=\frac{7-(x+2)}{x+2}=\frac{7}{x+2}-1$
Để $A$ min thì $\frac{7}{x+2}$ min
Điều này xảy ra khi $x+2$ là số nguyên âm lớn nhất
$\Rightarrow x+2=-1$
$\Rightarrow x=-3$. Khi đó: $A_{\min}=\frac{7}{-1}-1=-7-1=-8$
b.
$B=\frac{x^2-4x+10-8}{x^2-4x+10}=1-\frac{8}{x^2-4x+10}$
Để $B$ min thì $\frac{8}{x^2-4x+10}$ max
Điều này xảy ra khi $x^2-4x+10$ min
Mà: $x^2-4x+10=(x-2)^2+6\geq 6$ với mọi $x$
$\Rightarrow x^2-4x+10$ max = 6 khi $x=2$
Khi đó: $B_{\min}=1-\frac{8}{x^2-4x+10}=1-\frac{8}{2^2-4.2+10}=\frac{-1}{3}$

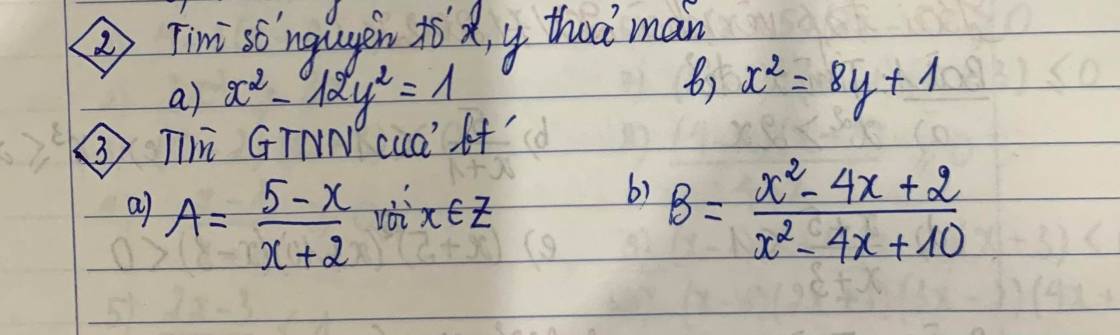




 giúp em 3 bài này với ạ em đang cần gấp chiều em hc ròi ạ ai làm đc bài nào thì gửi luôn giúp em ạ
giúp em 3 bài này với ạ em đang cần gấp chiều em hc ròi ạ ai làm đc bài nào thì gửi luôn giúp em ạ
 ai giải giúp em từ 3 đến bài 12 với ạ em đang cần gấp chiều em đi thi ạ
ai giải giúp em từ 3 đến bài 12 với ạ em đang cần gấp chiều em đi thi ạ









 MNG GIÚP EM BÀI 2 VỚI Ạ EM CẢM ƠN MNG NHIỀU Ạ
MNG GIÚP EM BÀI 2 VỚI Ạ EM CẢM ƠN MNG NHIỀU Ạ