A = \(\dfrac{1}{1+2}\) + \(\dfrac{1}{1+2+3}\) + \(\dfrac{1}{1+2+3+4}\)+......+\(\dfrac{1}{1+2+3+....+100}\)
A = \(\dfrac{1}{(1+2)\times2:2}\) + \(\dfrac{1}{(1+3)\times3:2}\) + ......+ \(\dfrac{1}{(1+100)\times100:2}\)
A = \(\dfrac{2}{2\times3}\) + \(\dfrac{2}{3\times4}\)+.....+ \(\dfrac{2}{100\times101}\)
A = 2 \(\times\) ( \(\dfrac{1}{2\times3}\) + \(\dfrac{1}{3\times4}\) +....+ \(\dfrac{1}{100\times101}\))
A = 2 \(\times\) ( \(\dfrac{1}{2}\) - \(\dfrac{1}{3}\) + \(\dfrac{1}{3}\) - \(\dfrac{1}{4}\) +......+ \(\dfrac{1}{100}\) - \(\dfrac{1}{101}\))
A = 2 \(\times\) ( \(\dfrac{1}{2}\) - \(\dfrac{1}{101}\))
A = 2 \(\times\) \(\dfrac{99}{202}\)
A = \(\dfrac{99}{101}\)

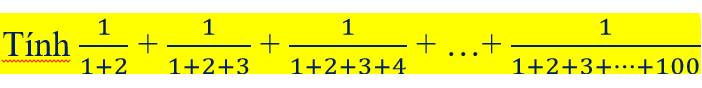 ai giải nhanh mình sẽ kết bạn và tick
ai giải nhanh mình sẽ kết bạn và tick









