Các câu hỏi tương tự
Cho hình 125 trong đó ABCD là hình chữ nhật, E là một điểm bất kì nằm trên đường chéo AC, FG // AD và HK // AB. Chứng minh rằng hai hình chữ nhật EFBK và EGDH có cùng diện tích.
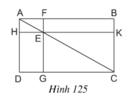
Cho hình chữ nhật ABCD. Qua E là một điểm bất kỳ nằm trên đường chéo AC, kẻ hai đường chéo FG//AD và HK//AB ( F ∈ AB, G ∈ DC, H ∈ AD, K ∈ DC ). Chứng minh rằng hai hình chữ nhật EFBK và EGDH có cùng diện tích.
Cho ABCD là hình chữ nhật trong đó E là điểm bất kỳ nằm trên đường chéo AC, FG // AD , HK // AB. Chứng minh diện tích EFBK = diện tích EGDH.
Bài 1: cho hình chữ nhật ABCD. E là điểm bất kì trên đường chéo AC. đường thẳng qua E, song song với AD cắtt AB, DC lần lượt tại F, G. đường thẳng qua E, song song với AB cắt AD, BC lần lượt tại H, K. chứng minh 2 hình chữ nhật EFBK và EGDH có cùng diện tích
Cho hình 125, trong đó ABCD là hình chữ nhật, E là một điểm bất kì nằm trên đường chéo AC, FG // AD, và HK // AB.
Cho hình chữ nhật ABCD. O là giao điểm hai đường chéo và một điểm P bất kì trên đường chéo BD (P nằm giữa O và D). Gọi M là điểm đối xứng của C qua P. a) Chứng minh tứ giác AMDB là hình thang. Xác định vị trí của P trên BD để AMDB là hình thang cân. b) Kẻ ME vuông góc AD, MF vuông góc BA. Chứng minh EF // AC và 3 điểm E, F, P thẳng hàng. c) Xác định vị trí P trên BD để tứ giác nối 4 điểm A, M, D, B là hình thang cân. d) Nếu hình chữ nhật ABCD có AB 2BC. Gọi K là điểm trên AB sao cho góc ADK $1...
Đọc tiếp
Cho hình chữ nhật ABCD. O là giao điểm hai đường chéo và một điểm P bất kì trên đường chéo BD (P nằm giữa O và D). Gọi M là điểm đối xứng của C qua P. a) Chứng minh tứ giác AMDB là hình thang. Xác định vị trí của P trên BD để AMDB là hình thang cân. b) Kẻ ME vuông góc AD, MF vuông góc BA. Chứng minh EF // AC và 3 điểm E, F, P thẳng hàng. c) Xác định vị trí P trên BD để tứ giác nối 4 điểm A, M, D, B là hình thang cân. d) Nếu hình chữ nhật ABCD có AB = 2BC. Gọi K là điểm trên AB sao cho góc ADK = $15^o$. Chứng minh tam giác CDK cân.
1. Trên hai cạnh của góc nhọn xOy, đặt các đoạn thẳng AB và CD bằng nhau (A giữa O và B, C nằm giữa O và D). I và E lần lượt là trung điểm của AC và BD. Chứng minh rằng đường thẳng IE song song với tia phân giác của góc xOy. Giúp mình với nha!!!2. Cho hình chữ nhật ABCD. Ta nối đỉnh A với một điểm E bất kỳ trên đường chéo DB rồi kéo dài và lấy trên đó một điểm F sao choFE AE . Từ E dựng đường song song với đường chéo AC, đường này cắt BC tại I, và cắt DC kéo dài tại K.a) Chứng minh: CF // DBb)...
Đọc tiếp
1. Trên hai cạnh của góc nhọn xOy, đặt các đoạn thẳng AB và CD bằng nhau (A giữa O và B, C nằm giữa O và D). I và E lần lượt là trung điểm của AC và BD. Chứng minh rằng đường thẳng IE song song với tia phân giác của góc xOy.
Giúp mình với nha!!!
2. Cho hình chữ nhật ABCD. Ta nối đỉnh A với một điểm E bất kỳ trên đường chéo DB rồi kéo dài và lấy trên đó một điểm F sao cho
FE = AE . Từ E dựng đường song song với đường chéo AC, đường này cắt BC tại I, và cắt DC kéo dài tại K.
a) Chứng minh: CF // DB
b) Chứng minh: tứ giác FICK là hình chữ nhật.
Bài 6. Cho hình chữ nhật ABCD. Nối C với một điểm E bất kỳ trên đường chéo
BD. Trên tia đối của tia EC lấy điểm F sao cho EF = EC. Vẽ FH và FK lần lượt
vuông góc với AB và AD. Chứng minh rằng:
a) Tứ giác AHFK là hình chữ nhật.
b) AF song song với BD và KH song song với AC.
Cho hình chữ nhật ABCD, M là một điểm bất kì nằm trong hình chữ nhật đó. Chứng minh MA + MC + MB + MD < AB+AD+AC.









