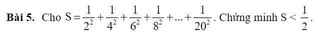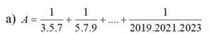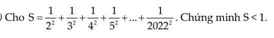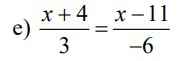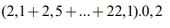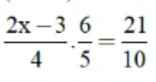\(S=\dfrac{1}{2^2}+\dfrac{1}{\left(2.2\right)^2}+\dfrac{1}{\left(2.3\right)^2}+...+\dfrac{1}{\left(2.10\right)^2}\)
\(=\dfrac{1}{2^2}+\dfrac{1}{2^2.2^2}+\dfrac{1}{2^2.3^2}+...+\dfrac{1}{2^2.10^2}\)
\(=\dfrac{1}{2^2}\left(1+\dfrac{1}{2^2}+\dfrac{1}{3^2}+...+\dfrac{1}{10^2}\right)\)
\(< \dfrac{1}{2^2}\left(1+\dfrac{1}{1.2}+\dfrac{1}{2.3}+...+\dfrac{1}{9.10}\right)\)
\(=\dfrac{1}{4}\left(1+1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+...+\dfrac{1}{9}-\dfrac{1}{10}\right)\)
\(=\dfrac{1}{4}\left(2-\dfrac{1}{10}\right)< \dfrac{1}{4}.2=\dfrac{1}{2}\) (đpcm)