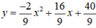a. Xét dấu của biểu thức f(x) = 2x(x+2)-(x+2)(x+1)
b. Lập bảng biến thiên và vẽ trong cùng một hệ tọa độ vuông góc đồ thị của các hàm số : y = 2x(x+2) ( C1 ) và y = (x+2)(x+1)(C2)
Tính tọa độ giao điểm A và B của (C1) và (C2).
c. Tính các hệ số a, b, c để hàm số y = ax2 + bx + c có giá trị lớn nhất bằng 8 và độ thị của nó đi qua A và B.
a) f(x) = 2x.(x+2) - (x+2)(x+1) = 2x2 + 4x - (x2 + 3x + 2) = x2 + x - 2
Tam thức x2 + x – 2 có hai nghiệm x1 = -2 và x2 = 1, hệ số a = 1 > 0.
Vậy:
+ f(x) > 0 nếu x > x2 = 1 hoặc x < x1 = -2, hay x ∈ (-∞; -2) ∪ (1; + ∞)
+ f(x) < 0 nếu x1 < x < x2 hay x ∈ (-2; 1)
+ f(x) = 0 nếu x = -2 hoặc x = 1.
b)
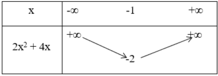
* Hàm số y = 2x(x+2) = 2x2 + 4x có đồ thị (C1) là parabol có:
+ Tập xác định: D = R
+ Đỉnh I1( -1; -2)
+ Trục đối xứng: x = -1
+ Giao điểm với trục tung tại gốc tọa độ.
+ Giao điểm với trục hoành tại O(0; 0) và M(-2; 0).
+ Bảng biến thiên:
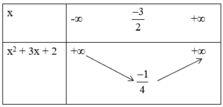
* Hàm số y = (x + 2)(x+1) = x2 + 3x + 2 có đồ thị (C2) là parabol có:
+ Tập xác định D = R.
+ Đỉnh 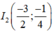
+ Trục đối xứng: x = -3/2
+ Giao với trục tung tại D(0; 2)
+ Giao với trục hoành tại M(-2; 0) và E(-1; 0)
+ Bảng biến thiên
* Đồ thị:
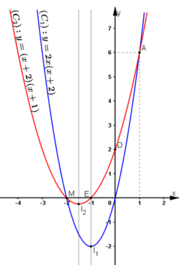
* Tìm tọa độ giao điểm:
Cách 1: Dựa vào đồ thị hàm số:
Nhìn vào đồ thị thấy (C1) cắt (C2) tại A(1; 6) và B ≡ M(-2; 0)
Cách 2: Tính:
Hoành độ giao điểm của (C1) và (C2) là nghiệm của phương trình:
2x(x + 2) = (x + 2)(x + 1)
⇔ (x + 2).2x – (x + 2)(x + 1) = 0
⇔ (x + 2).(2x – x – 1) = 0
⇔ (x + 2).(x – 1) = 0
⇔ x = -2 hoặc x = 1.
+ x = -2 ⇒ y = 0. Ta có giao điểm B(-2; 0)
+ x = 1 ⇒ y = 6. Ta có giao điểm A(1; 6).
c)
+ Đồ thị hàm số y = ax2 + bx + c đi qua điểm A(1; 6) và B(-2; 0)
⇔ tọa độ A và B thỏa mãn phương trình y = ax2 + bx + c
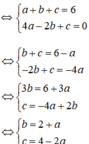
+ Ta có bảng biến thiên của hàm số y = ax2 + bx + c:
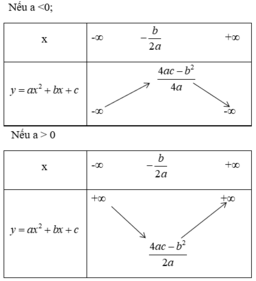
Nhận thấy y đạt giá trị lớn nhất bằng 8
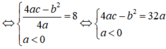
Thay b = 2 + a và c = 4 – 2a vào biểu thức 4ac – b2 = 32a ta được:
4.a.(4 – 2a) – (2 + a)2 = 32a
⇔ 16a – 8a2 – (a2 + 4a + 4) = 32a
⇔ 16a– 8a2 – a2 – 4a - 4 – 32a = 0
⇔ -9a2 - 20a - 4 = 0
⇔ a = -2 hoặc a = -2/9.
Nếu a = -2 ⇒ b = 0, c = 8, hàm số y = -2x2 + 8
Nếu a = -2/9 ⇒ b = 16/9, c = 40/9, hàm số