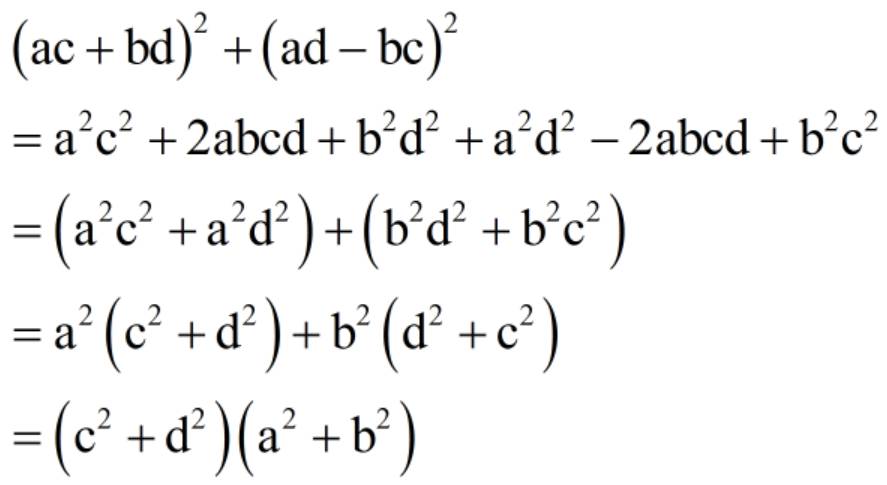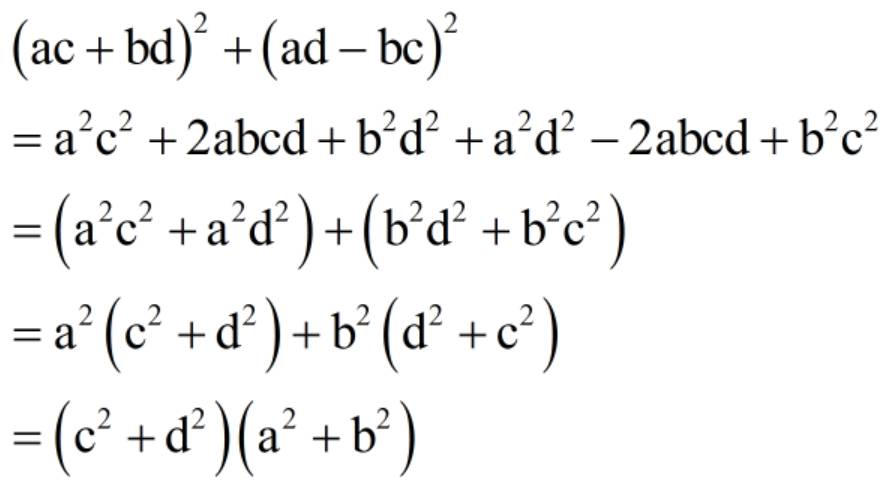Question

a) Chứng minh: (ac + bd)² + (ad – bc)² = (a² + b²)(c² + d²)

Answer 1

\begin{equation}
\begin{aligned}
& (a c+b d)^2+(a d-b c)^2 \\
& =a^2 c^2+2 a b c d+b^2 d^2+a^2 d^2-2 a b c d+b^2 c^2 \\
& =\left(a^2 c^2+a^2 d^2\right)+\left(b^2 d^2+b^2 c^2\right) \\
& =a^2\left(c^2+d^2\right)+b^2\left(d^2+c^2\right) \\
& =\left(c^2+d^2\right)\left(a^2+b^2\right)
\end{aligned}
\end{equation}

Answer 2

Answer 3

\(\left(ac+bd\right)^2+\left(ad-bc\right)^2\\ =a^2d^2+2abcd+b^2d^2+a^2d^2-2abcd+b^2c^2\\ =\left(a^2c^2+b^2c^2\right)+\left(b^2d^2+a^2d^2\right)\\ =c^2\left(a^2+b^2\right)+d^2\left(b^2+a^2\right)\\ =\left(a^2+b^2\right)\left(c^2+d^2\right)\)

Answer 4