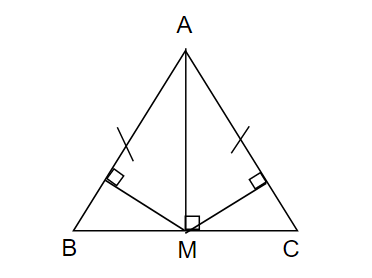
a. Xét tam giác vuông AMB và tam giác vuông AMC, có:
AB = AC ( ABC cân )
góc B = góc C ( ABC cân )
Vậy tam giác vuông AMB = tam giác vuông AMC ( cạnh huyền.góc nhọn)
b. Áp dụng định lý pitago vào tam giác vuông ABM, có:
\(AB^2=AM^2+BM^2\)
\(\Rightarrow BM=\sqrt{AB^2-AM^2}=\sqrt{15^2-12^2}=\sqrt{81}=9cm\)
c. Xét tam giác vuông AHM và tam giác vuông AKM, có:
góc HAM = góc KAM ( AH là đường cao cũng là đường phân giác )
AM: cạnh chung
Vậy tam giác vuông AHM = tam giác vuông AKM ( cạnh huyền.góc nhọn )
=> AH = AK ( 2 cạnh tương ứng ) (*)
d.(*) suy ra tam giác AHK cân tại A
Mà AM là đường phân giác => AM cũng là đường cao (1)
AM vuông với BC ( gt ) (2)
Từ (1) và (2) suy ra HK//BC