8/61
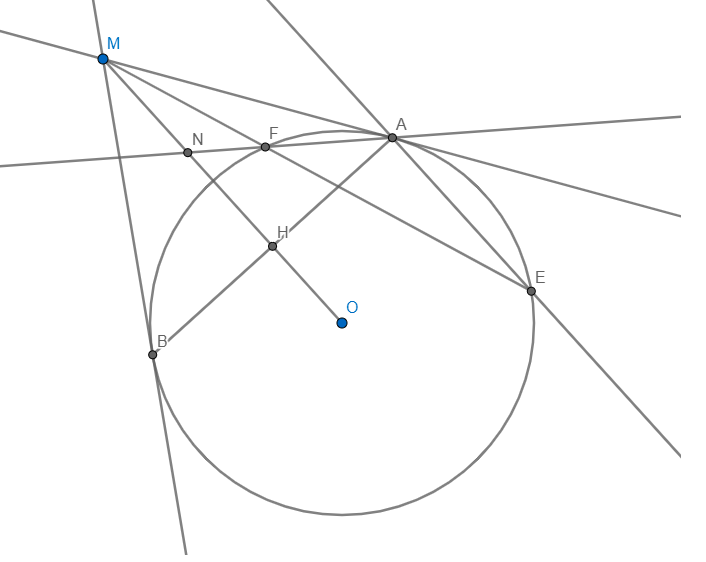
cho đường tròn tâm O , bán kính R . từ 1 điểm M ở ngìa đường tròn , kẻ 2 tiếp tuyến MA,MB với đường tròn
A/ chứng minh tứ giác MABO nội tiếp đường tròn
b/ qua A kẻ đường thẳng song song với MO cắt đường tròn tại E ( E khác A) , đường thẳng ME cắt đường tròn tại F ( F khác E ) , đường thẳng AF cắt MO tại N . H là giao đểm của MO và AB . chứng minh MN^2=NF.NA
thankkkkkkkkkkkkkkkk
a) Ta có: \(\angle MAO+\angle MBO=90+90=180\Rightarrow MAOB\) nội tiếp
b) Vì \(MO\parallel AE\) \(\Rightarrow\angle NMF=\angle MEA=\angle MAF\) (góc tạo bởi tiếp tuyến và dây cung bằng góc nội tiếp chắn cung đó)
Xét \(\Delta NFM\) và \(\Delta NMA:\) Ta có: \(\left\{{}\begin{matrix}\angle NMF=\angle NAM\\\angle MNAchung\end{matrix}\right.\)
\(\Rightarrow\Delta NFM\sim\Delta NMA\left(g-g\right)\Rightarrow\dfrac{NF}{NM}=\dfrac{NM}{NA}\Rightarrow NM^2=NF.NA\)