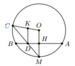
\(\Delta KCD\) là tam giác cân
Vì \(M\) là điểm chính giữa cung \(AB\)
\(OM\text{┴}AB\Rightarrow OM\) song song với \(KD\)
\(\Rightarrow\widehat{KDC}=\widehat{OMC}=\widehat{OCM}\Rightarrow\Delta KCD\) cân
Cho đường tròn tâm O và dây AB.Gọi M là điểm chính giữa của cung AB nhỏ. Vẽ đường kính MN cắt AB tại I. Lấy D thuộc dây AB, MD giao với đường trong (O) tại C.
a) c/m rằng : CDIN là tứ giác nội tiếp
b) c/m rằng: MC.MD có giá trị không đổi khi D di động trên dây AB
c) Gọi O’ là tâm đường tròn ngoại tiếp tam giác ACD. Chứng minh góc MAB = 1/2 góc AO’D
Cho đường tròn (O) và hai dây AB, AC. Gọi M, N lần lượt là điểm chính giữa của cung AB và cung AC. Đường thẳng MN cắt dây AB tại E và cắt dây AC tại H. Chứng minh tam giác AEH là tam giác cân.
Cho đường tròn (O) và hai dây AB, AC. Gọi M, N lần lượt là điểm chính giữa của cung AB và cung AC. Đường thẳng MN cắt dây AB tại E và cắt dây AC tại H. Chứng minh tam giác AEH là tam giác cân.
Cho đường tròn (O) ngoại tiếp tam giác nhọn ABC. Gọi M và N lần lượt là điểm chính giữa của cung nhỏ AB và cung nhỏ BC. Hai dây AN và CM cắt nhau tại điểm I. Dây MN cắt các cạnh AB và BC lần lượt tại các điểm H và K.
4) Gọi P, Q lần lượt là tâm của các đường tròn ngoại tiếp tam giác MBK, tam giác MCK và E là trung điểm của đoạn PQ. Vẽ đường kính ND của đường tròn (O) . Chứng minh ba điểm D, E, K thẳng hàng.
1 . Cho hình vuông ABCD. Gọi O là giao điểm của hai đường chéo. Qua điểm C kẻ đường thẳng Cx song song với BD; Cx cắt AB tại E.
a) Chứng minh tam giác ACE vuông cân
b) Gọi F là điểm đối xứng của O qua AB. Tứ giác AOBF là hình gì? Vì sao?
c) Giả sử APCQ là hình thoi có chung đường chéo AC với hình vuông ABCD. Hãy chứng tỏ 4 điểm P, D, B, Q thẳng hàng
Bài 2:Đường tròn tâm O và một dây AB của đường tròn đó. Các tiếp tuyến vẽ từ A và B của đường tròn cắt nhau tại C. D là một điểm trên đường tròn có đường kính OC (D khác A và B). CD cắt cung AB của đường tròn (O) tại E (E nằm giữa C và D). Chứng minh:
a) Góc BED = góc DAE
b) DE2 = DA.DB
Bài 3:Cho (O) dây AB vuông góc dây CD M là trung điểm BC. Chứng minh rằng OM=1/2AD
Cho đường tròn tâm O và dây AB.Gọi M là điểm chính giữa của cung AB nhỏ. Vẽ đường kính MN cắt AB tại I. Lấy D thuộc dây AB, MD giao với đường trong (O) tại C.
a) c/m rằng : CDIN là tứ giác nội tiếp
b) c/m rằng: MC.MD có giá trị không đổi khi D di động trên dây AB
c) Gọi O’ là tâm đường tròn ngoại tiếp tam giác ACD. Chứng minh gócˆMAB=1/2 góc AO’D
cho tam giác ABC nội tiếp đường tròn (O). gọi M là điểm chính giữa cung AB. Vẽ dây MN cắt AC tại K. Chứng minh KM=KC;KN=KA.
Cho đường tròn (o), dây cung AB trên tia đối của tia BA lấy điểm C ,gọi D là điểm chính giữa cung lớn AB kẻ đường kính DE cắt dây AB tại I. Tia CD cắt đường tròn tại điểm thứ hai H.Các dây AB và EH cắt nhau tại K.
a) Chứng minh rằng tứ giác DHKI nội tiếp
b) Chứng minh CB.CA=CI.CK
c) chứng minh tia HC là tia phân giác góc ngoài đỉnh H của tg AHB
Cho đường tròn (O; R), dây AB. Trên cung lớn AB lấy điểm C sao cho A < CB. Các đường cao AE và BF của tam giác ABC cắt nhau tại I.
d) Đường tròn ngoại tiếp tam giác CEF cắt đường tròn (O; R) tại điểm thứ hai là K (K khác C). Vẽ đường kính CD của (O; R). Gọi P là trung điểm của AB. Chứng minh rằng ba điểm K, P, D thẳng hàng.
