1. Cho a,b,c>0 và a+b+c=1. Tìm giá trị nhỏ nhất của:
\(M=\dfrac{1}{1-2\left(ab+bc+ca\right)}+\dfrac{1}{abc}\)
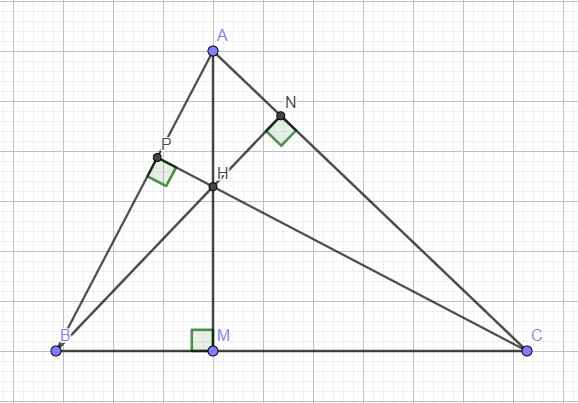
2. Cho tam giác ABC nhọn có các đường cao AM, BN, CP cắt nhau tại H.
a) Chứng minh: AB.BP+AC.CN=BC2
b) Cho B, C cố định A thay đổi. Tìm vị trí điểm A để: MH.MA đạt max ?
c) Gọi S,S1,S2,S3 lần luợt là diện tích các tam giác ABC, APN, BMP, CMN.
Chứng minh: \(S_1.S_2.S_3\text{≤}\dfrac{1}{64}S_3\)
Tham khảo:
Tìm GTNN của M=1/1-2(ab+bc+ac)+1/abc - thu phương
1.
\(M=\dfrac{1}{1-2\left(ab+bc+ca\right)}+\dfrac{a+b+c}{abc}=\dfrac{1}{1-2\left(ab+bc+ca\right)}+\dfrac{1}{ab}+\dfrac{1}{bc}+\dfrac{1}{ca}\)
\(M\ge\dfrac{1}{1-2\left(ab+bc+ca\right)}+\dfrac{9}{ab+bc+ca}=\dfrac{1}{1-2\left(ab+bc+ca\right)}+\dfrac{1}{ab+bc+ca}+\dfrac{1}{ab+bc+ca}+\dfrac{7}{ab+bc+ca}\)
\(M\ge\dfrac{9}{1-2\left(ab+bc+ca\right)+2\left(ab+bc+ca\right)}+\dfrac{7}{\dfrac{1}{3}\left(a+b+c\right)^2}=9+21=30\)
2.
a. Hai tam giác vuông BCN và ACM đồng dạng (chung góc C)
\(\Rightarrow\dfrac{BC}{AC}=\dfrac{CN}{CM}\Rightarrow CN.AC=BC.CM\) (1)
Hai tam giác vuông ABM và CBP đồng dạng (chung góc B) (1')
\(\Rightarrow\dfrac{AB}{BC}=\dfrac{BM}{BP}\Rightarrow AB.BP=BC.BM\) (2)
Cộng vế (1) và (2):
\(AB.BP+AC.CN=BC\left(CM+BM\right)=BC^2\)
b.
Từ (1') \(\Rightarrow\widehat{BAM}=\widehat{BCP}\Rightarrow\) hai tam giác vuông ABM và CHM đồng dạng
\(\Rightarrow\dfrac{AM}{CM}=\dfrac{BM}{HM}\Rightarrow AM.HM=BM.CM\le\dfrac{1}{4}\left(BM+CM\right)^2=\dfrac{1}{4}BC^2\)
Dấu "=" xảy ra khi và chỉ khi \(BM=CM\) hay tam giác ABC cân tại A
\(\Rightarrow\) A nằm trên trung trực BC
Câu c nhìn là thấy đề sai, \(\Leftrightarrow S_1S_2\le\dfrac{1}{64}\) chỉ cần tam giác ABC đủ lớn thì \(S_1;S_2>1\) BĐT này sẽ sai ngay