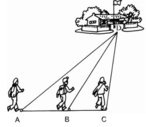
Dễ mà, xem mình giải nè:
Trong tam giác BCD có:
góc ACD là góc tù=> BD là cạch lớn nhất của tam giác BCD ; hay BD>CD (1)
Vì góc ABD là góc ngoài của tam giác BCD=> góc ABD > góc ACD
Mà góc ACD là góc tù=> góc BCD là góc tù
Trong tam giác ABD có góc ABD là góc tù
=> AD là cạch lớn nhất của tam giác ABD
hay AD>BD (2)
Từ (1) và (2) => AD>BD>CD
Vậy Người đi xa nhất là Hạnh
Người đi gần nhất là Trang
Vì .ACD = 900 nên ∆DCB có
=> BD > CD (1)
∆ABD có DBA là góc ngoài của ∆DCB
=>DBA > DCB
nên DBA là góc lớn nhất (vì DCB tù)
=> AD > BD (2)
Từ (1) và (2) => AD > BD >CD
Vậy Hạnh đi xa nhất, Trang đi gần nhất
Vì . = 900 nên ∆DCB có
=> BD > CD (1)
∆ABD có là góc ngoài của ∆DCB
=> >
nên là góc lớn nhất (vì tù)
=> AD > BD (2)
Từ (1) và (2) => AD > BD >CD
Vậy Hạnh đi xa nhất, Trang đi gần nhất
1 trong 2 canh
Trong tam giác DBC có góc C là góc tù (gt) ⇒ DB > DC (1) và có góc ∠B1 nhọn.
Ta có ∠B1 + ∠B2 = 1800 (kề bù)
mà ∠B1 <900 (cmt) ⇒ ∠B2 > 900
Trong ΔDAB có ∠B2 là góc tù (cmt) ⇒ DA > DB (2)
Từ (1) và (2) ta có DA > DB > DC
Vậy bạn Hạnh đi xa nhất; bạn Trang đi gần nhất.
Vì . = 900 nên ∆DCB có
=> BD > CD (1)
∆ABD có là góc ngoài của ∆DCB
=> >
nên là góc lớn nhất (vì tù)
=> AD > BD (2)
Từ (1) và (2) => AD > BD >CD
Vậy Hạnh đi xa nhất, Trang đi gần nhất
ban hanh di xa nhat ; bn trang di gan nhat