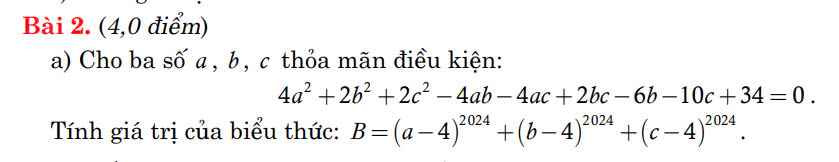\(\Leftrightarrow4a^2+\left(b+c\right)^2-4a\left(b+c\right)+\left(b^2-6b+9\right)+\left(c^2-10c+25\right)=0\)
\(\Leftrightarrow\left(2a-b-c\right)^2+\left(b-3\right)^2+\left(c-5\right)^2=0\)
Do \(\left\{{}\begin{matrix}\left(2a-b-c\right)^2\ge0\\\left(b-3\right)^2\ge0\\\left(c-5\right)^2\ge0\end{matrix}\right.\); \(\forall a;b;c\)
\(\Rightarrow\left(2a-b-c\right)^2+\left(b-3\right)^2+\left(c-5\right)^2\ge0\)
Dấu "=" xảy ra khi và chỉ khi:
\(\left\{{}\begin{matrix}2a-b-c=0\\b-3=0\\c-5=0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}a=4\\b=3\\c=5\end{matrix}\right.\)
\(\Rightarrow B=0+1+1=2\)
Đúng 0
Bình luận (0)
