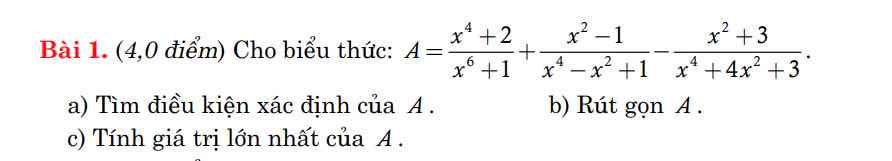a.
ĐKXĐ: \(x\in R\)
b.
\(A=\dfrac{x^4+2}{\left(x^2+1\right)\left(x^4-x^2+1\right)}+\dfrac{x^2-1}{x^4-x^2+1}-\dfrac{x^2+3}{\left(x^2+1\right)\left(x^2+3\right)}\)
\(=\dfrac{x^4+2}{\left(x^2+1\right)\left(x^4-x^2+1\right)}+\dfrac{x^2-1}{x^4-x^2+1}-\dfrac{1}{x^2+1}\)
\(=\dfrac{x^4+2}{\left(x^2+1\right)\left(x^4-x^2+1\right)}+\dfrac{\left(x^2-1\right)\left(x^2+1\right)}{\left(x^2+1\right)\left(x^4-x^2+1\right)}-\dfrac{x^4-x^2+1}{\left(x^2+1\right)\left(x^4-x^2+1\right)}\)
\(=\dfrac{x^4+2+\left(x^2-1\right)\left(x^2+1\right)-\left(x^4-x^2+1\right)}{\left(x^2+1\right)\left(x^4-x^2+1\right)}\)
\(=\dfrac{x^4+x^2}{\left(x^2+1\right)\left(x^4-x^2+1\right)}=\dfrac{x^2\left(x^2+1\right)}{\left(x^2+1\right)\left(x^4-x^2+1\right)}\)
\(=\dfrac{x^2}{x^4-x^2+1}\)
c.
\(A=\dfrac{x^4-x^2+1-\left(x^4-2x^2+1\right)}{x^4-x^2+1}=1-\dfrac{\left(x^2-1\right)^2}{\left(x^2-\dfrac{1}{2}\right)^2+\dfrac{3}{4}}\le1\)
\(A_{max}=1\) khi \(x=\pm1\)