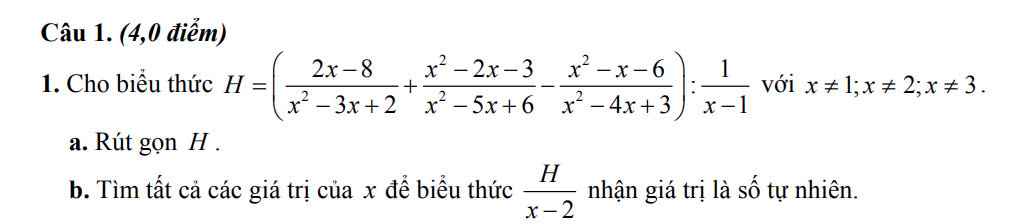a.
\(H=\left(\dfrac{2x-8}{\left(x-1\right)\left(x-2\right)}+\dfrac{\left(x+1\right)\left(x-3\right)}{\left(x-2\right)\left(x-3\right)}-\dfrac{\left(x+2\right)\left(x-3\right)}{\left(x-1\right)\left(x-3\right)}\right)\left(x-1\right)\)
\(=\left(\dfrac{2x-8}{\left(x-1\right)\left(x-2\right)}+\dfrac{x+1}{x-2}-\dfrac{x+2}{x-1}\right)\left(x-1\right)\)
\(=\left(\dfrac{2x-8}{\left(x-1\right)\left(x-2\right)}+\dfrac{\left(x+1\right)\left(x-1\right)}{\left(x-1\right)\left(x-2\right)}-\dfrac{\left(x+2\right)\left(x-2\right)}{\left(x-1\right)\left(x-2\right)}\right)\left(x-1\right)\)
\(=\left(\dfrac{2x-8+\left(x^2-1\right)-\left(x^2-4\right)}{\left(x-1\right)\left(x-2\right)}\right)\left(x-1\right)\)
\(=\left(\dfrac{2x-5}{\left(x-1\right)\left(x-2\right)}\right)\left(x-1\right)=\dfrac{2x-5}{x-2}\)
b.
Đặt \(P=\dfrac{H}{x-2}=\dfrac{2x-5}{\left(x-2\right)^2}\)
Do P là số tự nhiên \(\Rightarrow P\ge0\)
Đồng thời:
\(P=\dfrac{2x-5}{\left(x-2\right)^2}=\dfrac{x^2-4x+4-x^2+6x-9}{\left(x-2\right)^2}=1-\left(\dfrac{x-3}{x-2}\right)^2\le1\)
\(\Rightarrow0\le P\le1\)
Mà P là số tự nhiên \(\Rightarrow\left[{}\begin{matrix}P=0\\P=1\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}x=\dfrac{5}{2}\\x=3\end{matrix}\right.\)