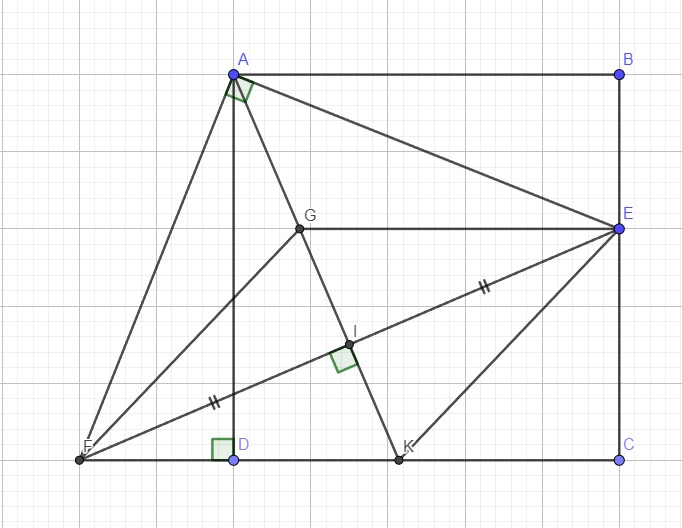
a.
Xét hai tam giác ADF và ABE có:
\(\left\{{}\begin{matrix}\widehat{ADF}=\widehat{ABE}=90^0\\AD=AB\\\widehat{DAF}=\widehat{BAE}\left(\text{cùng phụ }\widehat{DAE}\right)\end{matrix}\right.\)
\(\Rightarrow\Delta ADF=\Delta ABE\left(g.c.g\right)\)
\(\Rightarrow AE=AF\)
\(\Rightarrow\Delta AEF\) vuông cân tại A
\(\Rightarrow AI\) là trung tuyến đồng thời là đường cao
\(\Rightarrow AI\perp EF\) hay \(GK\perp EF\) (1)
Xét 2 tam giác FIK và EIG có:
\(\left\{{}\begin{matrix}\widehat{FIK}=\widehat{EIG}\left(\text{đối đỉnh}\right)\\IF=IE\left(gt\right)\\\widehat{IFK}=\widehat{IEG}\left(\text{so le trong}\right)\end{matrix}\right.\)
\(\Rightarrow\Delta FIK=\Delta EIG\left(g.c.g\right)\Rightarrow EG=FK\) (2)
Mà theo gt \(EG||AB\Rightarrow EG||FK\) (3)
(2);(3) \(\Rightarrow EGFK\) là hình bình hành (4)
(1);(4) \(\Rightarrow EGFK\) là hình thoi
b.
Xét 2 tam giác AEF và IAF có:
\(\left\{{}\begin{matrix}\widehat{AFE}\text{ chung}\\\widehat{FAE}=\widehat{FIA}=90^0\end{matrix}\right.\)
\(\Rightarrow\Delta AEF\sim\Delta IAF\left(g.g\right)\Rightarrow\dfrac{AF}{IF}=\dfrac{EF}{AF}\Rightarrow AF^2=IF.EF\) (5)
Xét hai tam giác FIK và FCE có:
\(\left\{{}\begin{matrix}\widehat{FIK}=\widehat{FCE}=90^0\\\widehat{IFK}\text{ chung}\end{matrix}\right.\) \(\Rightarrow\Delta FIK\sim\Delta FCE\left(g.g\right)\)
\(\Rightarrow\dfrac{IF}{FC}=\dfrac{FK}{EF}\Rightarrow FK.FC=IF.EF\) (6)
(5);(6) \(\Rightarrow AF^2=FK.FC\)