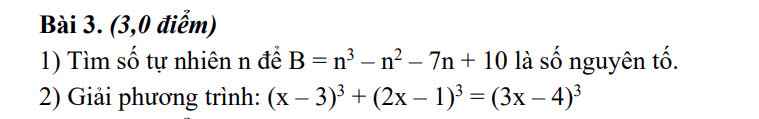a.
\(B=n^3-n^2-7n+10=\left(n-2\right)\left(n^2+n-5\right)\)
- Với \(n=0\Rightarrow B=10\) ko phải SNT (loại)
- Với \(n=1\Rightarrow B=3\) là SNT (thỏa mãn)
- Với \(n=2\Rightarrow B=0\) ko phải SNT (ko thỏa mãn)
Với \(n>2\Rightarrow\left\{{}\begin{matrix}n-2>0\\n^2+n-5>0\end{matrix}\right.\)
Để B là số nguyên tố thì:
TH1: \(n-2=1\) và \(n^2+n-5\) là SNT
Với \(n-2=1\Rightarrow n=3\)
Khi đó \(n^2+n-5=3^2+3-5=7\) là SNT (thỏa mãn)
TH2: \(n-2\) là SNT và \(n^2+n-5=1\)
Từ \(n^2+n-5=1\Leftrightarrow n^2+n-6=0\Rightarrow n=2\) (ko thỏa mãn, đã kiểm tra ở trên)
Vậy \(n=\left\{1;3\right\}\)
b.
\(\left(x-3\right)^3+\left(2x-1\right)^3=\left(3x-4\right)^3\)
Đặt \(\left\{{}\begin{matrix}x-3=a\\2x-1=b\end{matrix}\right.\) \(\Rightarrow3x-4=a+b\)
Phương trình trở thành:
\(a^3+b^3=\left(a+b\right)^3\)
\(\Leftrightarrow a^3+b^3=a^3+b^3+3ab\left(a+b\right)\)
\(\Leftrightarrow3ab\left(a+b\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}a=0\\b=0\\a+b=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x-3=0\\2x-1=0\\3x-4=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=3\\x=\dfrac{1}{2}\\x=\dfrac{4}{3}\end{matrix}\right.\)