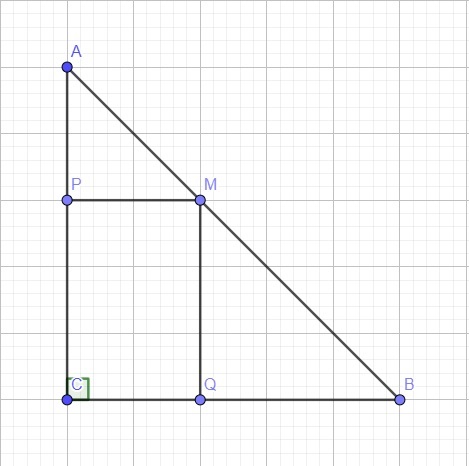
Do \(PM||BC\) mà \(Q\in BC\Rightarrow PM||CQ\) (1)
Cũng do \(PM||BC\), áp dụng định lý Thales:
\(\dfrac{AP}{AC}=\dfrac{PM}{BC}\) (2)
Mà theo giả thiết ABC vuông cân tại C nên \(AC=BC\)
\(\Rightarrow\dfrac{AP}{AC}=\dfrac{CQ}{BC}\) (3)
(2);(3) \(\Rightarrow\dfrac{CQ}{BC}=\dfrac{PM}{BC}\Rightarrow CQ=PM\) (4)
(1);(4) \(\Rightarrow PCQM\) là hình bình hành (5)
Lại có \(\Delta ABC\) vuông cân tại C \(\Rightarrow\widehat{C}=90^0\) (6)
(5);(6) \(\Rightarrow PCQM\) là hình chữ nhật
Đúng 0
Bình luận (0)
