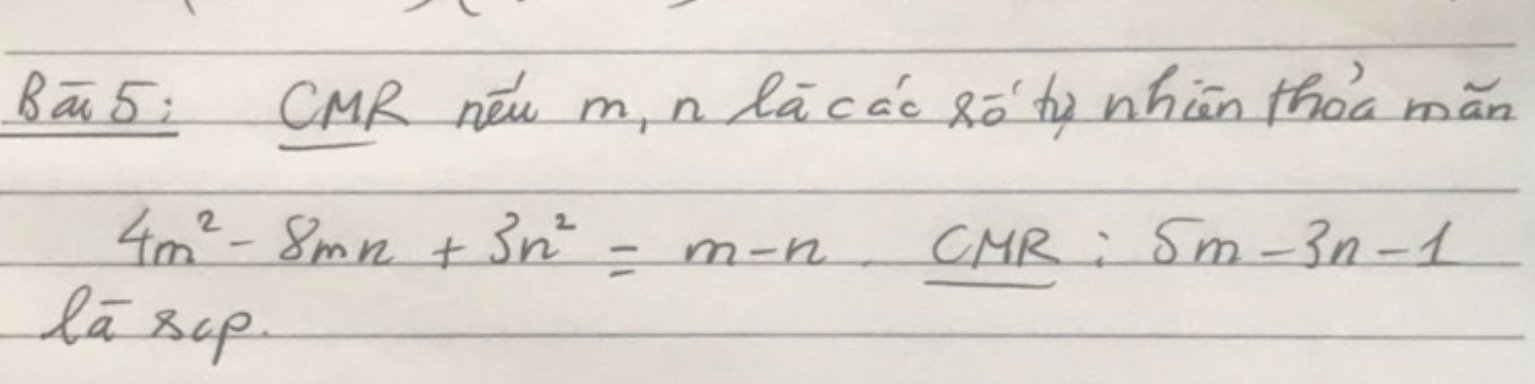Bổ đề: Cho a,b,n là các số nguyên dương. Nếu \(gcd\left(a,b\right)=1\) và \(ab=n^2\), thì a,b là các số chính phương.
Chứng minh: Theo Định lí cơ bản về số học, ta có thể giả sử a,b lần lượt có các phân tích thành thừa số nguyên tố như sau: \(\left\{{}\begin{matrix}a=p_1^{a_1}...p_k^{a_k}\\b=q_1^{b_1}...q_l^{b_l}\end{matrix}\right.\), trong đó \(\left(p_i\right),\left(q_j\right)\) là dãy tăng các số nguyên tố, với \(a_i,b_j>0\), \(i=\overline{1,k};j=\overline{1,l}\).
Do \(gcd\left(a,b\right)=1\) nên \(p_i\ne q_j\). Ta có:
\(ab=p_1^{a_1}...p_k^{a_k}q_1^{b_1}...q_l^{b_l}\). Mặt khác do ab là số chính phương nên \(a_i,b_j⋮2\). Do đó a,b là các số chính phương (hoàn tất chứng minh).
Quay lại bài toán, ta có:
\(4m^2-8mn+3n^2=m-n\)
\(\Leftrightarrow4\left(m-n\right)^2-\left(m-n\right)=n^2\)
\(\Leftrightarrow\left(m-n\right)\left(4m-4n-1\right)=n^2\)
Đặt \(gcd\left(m-n,4m-4n-1\right)=d\). Khi đó \(\left\{{}\begin{matrix}\left(m-n\right)⋮d\\\left(4m-4n-1\right)⋮d\end{matrix}\right.\Rightarrow1⋮d\Rightarrow d=1\)
Do đó \(gcd\left(m-n,4m-4n-1\right)=1\). Áp dụng bổ đề trên, ta có m-n là số chính phương.
Mặt khác, biến đổi cách khác, ta có:
\(\)\(\left(m-n\right)\left(4m-4n-1\right)=n^2\)
\(\Leftrightarrow\left(m-n\right)\left(5m-3n-1-m-n\right)=n^2\)
\(\Leftrightarrow\left(m-n\right)\left(5m-3n-1\right)=m^2\).
Do m-n là số chính phương nên 5m-3n-1 cũng là số chính phương.