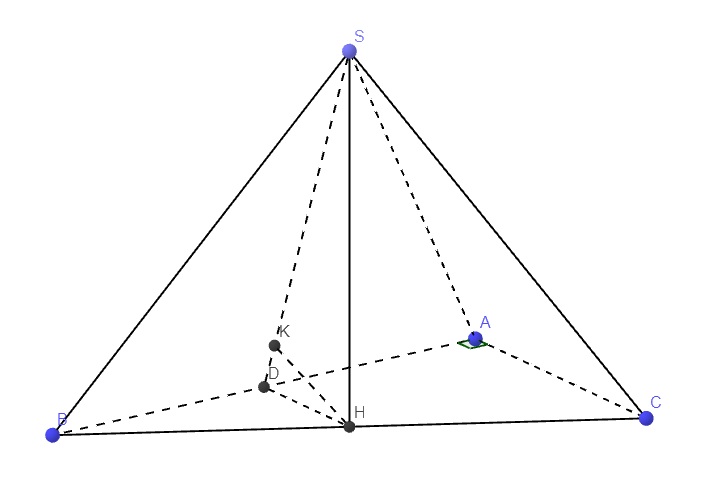
Gọi H là trung điểm BC \(\Rightarrow SH\perp BC\) (do SBC đều)
Mà \(\left\{{}\begin{matrix}BC=\left(SBC\right)\cap\left(ABC\right)\\\left(SBC\right)\perp\left(ABC\right)\end{matrix}\right.\) \(\Rightarrow SH\perp\left(ABC\right)\)
Từ H kẻ \(HD\perp AB\), từ H kẻ \(HK\perp SD\)
\(\Rightarrow HK\perp\left(SAB\right)\Rightarrow HK=d\left(H;\left(SAB\right)\right)\)
\(AC=BC.sinB=\dfrac{a}{2}\Rightarrow HD=\dfrac{1}{2}AC=\dfrac{a}{4}\) (đường trung bình)
\(SH=\dfrac{a\sqrt{3}}{2}\) (trung tuyến tam giác đều cạnh a)
Hệ thức lượng: \(HK=\dfrac{HD.SH}{\sqrt{HD^2+SH^2}}=\dfrac{a\sqrt{39}}{26}\)
\(\left\{{}\begin{matrix}CH\cap\left(SBC\right)=B\\CB=2HB\end{matrix}\right.\) \(\Rightarrow d\left(C;\left(SAB\right)\right)=2d\left(H;\left(SAB\right)\right)=2HK=\dfrac{a\sqrt{39}}{13}\)