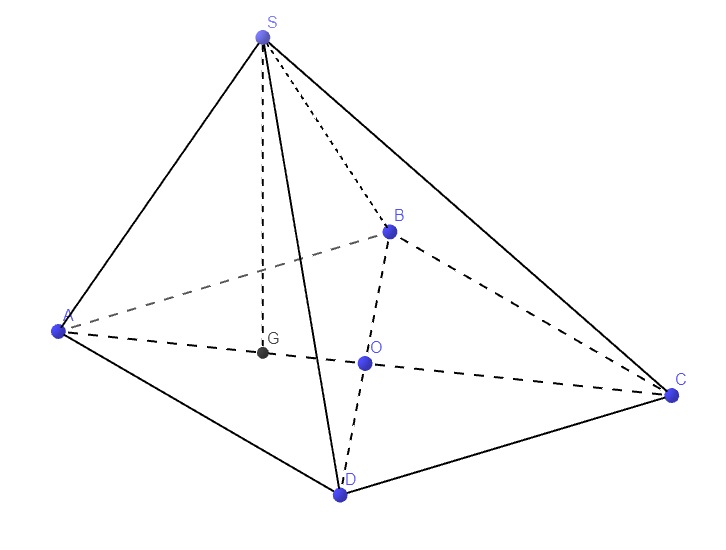
a.
\(\left\{{}\begin{matrix}AB=AD\left(gt\right)\\\widehat{DAB}=60^0\end{matrix}\right.\) \(\Rightarrow\Delta ABD\) đều
\(\Rightarrow\) Tâm đường tròn ngoại tiếp ABD trùng trọng tâm ABD
Hay G là tâm đường tròn ngoại tiếp tam giác ABD
Do \(SA=SB=SD\Rightarrow\) hình chiếu vuông góc của S lên (ABCD) trùng tâm đường tròn ngoại tiếp tam giác ABD
\(\Rightarrow SG\perp\left(ABCD\right)\)
b.
\(S_{\Delta BCD}=\dfrac{a^2\sqrt{3}}{4}\) (tam giác đều cạnh a)
Gọi O là trung điểm BD \(\Rightarrow AO=\dfrac{a\sqrt{3}}{2}\) (trung tuyến tam giác đều)
\(\Rightarrow AG=\dfrac{2}{3}AO=\dfrac{a\sqrt{3}}{3}\) (t/c trọng tâm)
\(\Rightarrow SG=\sqrt{SA^2-AO^2}=\dfrac{a\sqrt{33}}{3}\)
\(V_{S.BCD}=\dfrac{1}{3}SG.S_{\Delta BCD}=\dfrac{a^3\sqrt{11}}{12}\)