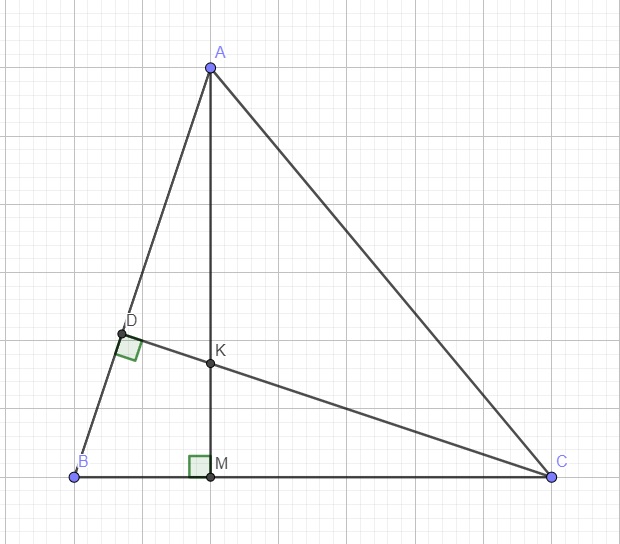
6.
a. Xét hai tam giác ABM và CBD có:
\(\left\{{}\begin{matrix}\widehat{B}-chung\\\widehat{AMB}=\widehat{CDB}=90^0\end{matrix}\right.\)
\(\Rightarrow\Delta ABM\sim\Delta CBD\left(g.g\right)\)
b.
Xét hai tam giác AKD và CKM có:
\(\left\{{}\begin{matrix}\widehat{ADK}=\widehat{CMK}=90^0\\\widehat{AKD}=\widehat{CKM}\left(\text{đối đỉnh}\right)\end{matrix}\right.\)
\(\Rightarrow\Delta AKD\sim\Delta CKM\left(g.g\right)\)
c.
Từ câu a, do \(\Delta ABM\sim\Delta CBD\Rightarrow\dfrac{AB}{CB}=\dfrac{MB}{DB}\)
\(\Rightarrow AB.DB=CB.MB\)
3.
Gọi độ dài quãng đường AB là x (km) với x>0
Thời gian ô tô đi từ A đến B là: \(\dfrac{x}{60}\) giờ
Độ dài quãng đường về là: \(x+10\) (km)
Thời gian về là: \(\dfrac{x+10}{40}\) giờ
Do thời gian về nhiều hơn thời gian đi là 45 phút = 3/4 giờ nên ta có pt:
\(\dfrac{x+10}{40}-\dfrac{x}{60}=\dfrac{3}{4}\)
\(\Leftrightarrow\dfrac{x}{120}=1\)
\(\Leftrightarrow x=120\left(km\right)\)
4.
Diện tích đáy \(S_{đáy}=15,06\left(cm^2\right)\), thể tích \(V=32,16\left(cm^3\right)\)
Áp dụng công thức:
\(V=\dfrac{1}{3}S_{đáy}.h\Rightarrow h=\dfrac{3V}{S_{đáy}}=\dfrac{3.32,16}{15,06}=6,406\left(cm\right)\)
5.
Đổi 30,4mm=3,04cm
Thể tích khối rubik là:
\(V=\dfrac{1}{3}S.h=\dfrac{1}{3}.15,06.3,04=15,2608\left(cm^3\right)\)