Gọi thời gian để người thứ nhất và người thứ hai làm riêng xong công việc lần lượt là x,y (giờ) (x,y>2)
=> Trong một giờ, người thứ nhất làm được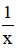 
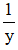
(công việc); người thứ hai làm được 
(công việc).
+ Cả hai người cùng làm sẽ hoàn thành công việc trong 2 giờ nên ta có phương trình \(2\left(\dfrac{1}{x}+\dfrac{1}{y}\right)=1\) (1)
+ Nếu hai người làm riêng thì thời gian người thứ hai làm xong việc nhiều hơn người thứ nhất là 3 giờ nên ta có phương trình y - x = 3 (2)
Từ (2) => y = x+3
Thay vào (1) ta được \(2\left(\dfrac{1}{x}+\dfrac{1}{x+3}\right)=1\Leftrightarrow...\Leftrightarrow x=3\)
=> y=x+3=6
Vậy người thứ nhất làm riêng thì sau 3 giờ xong công việc, người thứ hai làm riêng thì sau 6 giờ xong công việc
Lời giải:
Giả sử người thứ nhất và thứ hai làm lần lượt trong $a$ và $b$ giờ sẽ xong việc.
Trong 1 giờ, người 1 làm được $\frac{1}{a}$ công việc, người 2 làm được $\frac{1}{b}$ công việc.
Theo bài ra ta có:
$\frac{2}{a}+\frac{2}{b}=1$
$b-a=3$
Giải HPT gồm 2 PT trên thì $a=3; b=6$ (giờ)
Vậy..........