Question

Answer 1

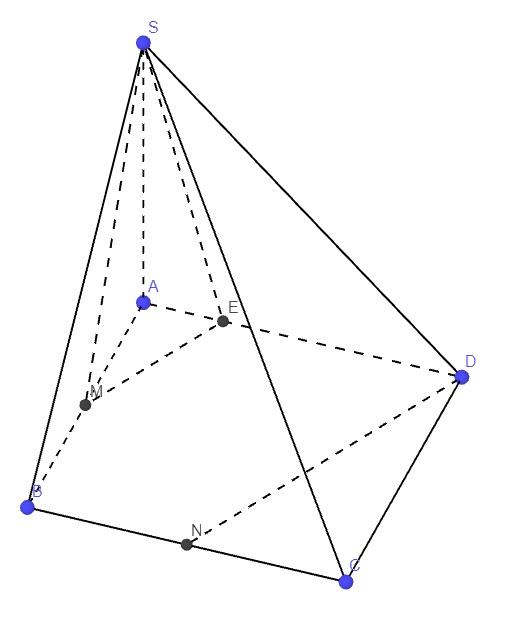
Trong mp (ABCD), qua M kẻ đường thẳng song song DN cắt AD tại E

\(\Rightarrow cos\widehat{\left(SM;DN\right)}=cos\widehat{\left(SM;ME\right)}=\left|cos\widehat{SME}\right|\)

\(SA=\sqrt{SB^2-AB^2}=a\)

\(AE=AM.tan\widehat{AME}=AM.tan\widehat{CDN}=\dfrac{AB}{2}.\dfrac{CN}{CD}=\dfrac{a}{2}\)

\(ME=\sqrt{AM^2+AE^2}=\dfrac{a\sqrt{5}}{2}\)

\(SM=\sqrt{SA^2+AM^2}=a\sqrt{2}\)

\(SE=\sqrt{SA^2+AE^2}=\dfrac{a\sqrt{5}}{2}\)

Áp dụng định lý hàm cosin:

\(cos\widehat{SME}=\dfrac{SM^2+ME^2-SE^2}{2SM.ME}=\dfrac{\sqrt{10}}{5}\)

Answer 2