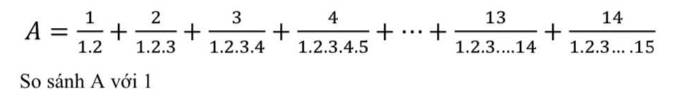Question

Answer 1

giúp tớ với , mình đang cần gấp

 

Answer 2

\(A=\dfrac{1}{2!}+\dfrac{2}{3!}+\dfrac{3}{4!}+\dfrac{4}{5!}+...+\dfrac{14}{15!}\)

\(A=\dfrac{2-1}{2!}+\dfrac{3-1}{3!}+\dfrac{4-1}{4!}+...+\dfrac{15-1}{15!}\)

\(A=\dfrac{2}{2!}-\dfrac{1}{2!}+\dfrac{3}{3!}-\dfrac{1}{3!}+\dfrac{4}{4!}-\dfrac{1}{4!}+...+\dfrac{15}{15!}-\dfrac{1}{15!}\)

\(A=1+\dfrac{1}{2!}+\dfrac{1}{3!}+\dfrac{1}{4!}+...+\dfrac{1}{14!}-\left(\dfrac{1}{2!}+\dfrac{1}{3!}+...+\dfrac{1}{15!}\right)\)

\(A=1-\dfrac{1}{15!}< 1\)

Vậy \(A< 1\)