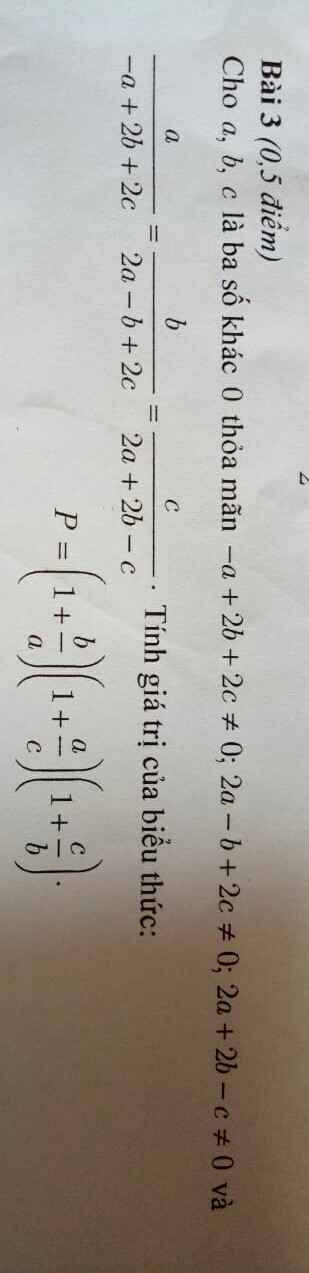Áp dụng tính chất dãy tỉ số bằng nhau:
\(\dfrac{a}{-a+2b+2c}+\dfrac{b}{2a-b+2c}+\dfrac{c}{2a+2b-c}=\dfrac{a+b+c}{3a+3b+3c}=\dfrac{1}{3}\)
\(\Rightarrow\left\{{}\begin{matrix}\dfrac{a}{-a+2b+2c}=\dfrac{1}{3}\\\dfrac{b}{2a-b+2c}=\dfrac{1}{3}\\\dfrac{c}{2a+2b-c}=\dfrac{1}{3}\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}3a=-a+2b+2c\\3b=2a-b+2c\\3c=2a+2b-c\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}6a=2a+2b+2c\\6b=2a+2b+2c\\6c=2a+2b+2c\end{matrix}\right.\)
\(\Rightarrow6a=6b=6c\Rightarrow a=b=c\)
\(\Rightarrow P=\left(1+\dfrac{a}{a}\right)\left(1+\dfrac{a}{a}\right)\left(1+\dfrac{a}{a}\right)=2.2.2=8\)