a.
\(\dfrac{x+1}{4}=\dfrac{9}{x+1}\Rightarrow\left(x+1\right)^2=36\)
\(\Rightarrow\left[{}\begin{matrix}x+1=6\\x+1=-6\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=5\\x=-7\end{matrix}\right.\)
Do x âm nên \(x=-7\)
b.
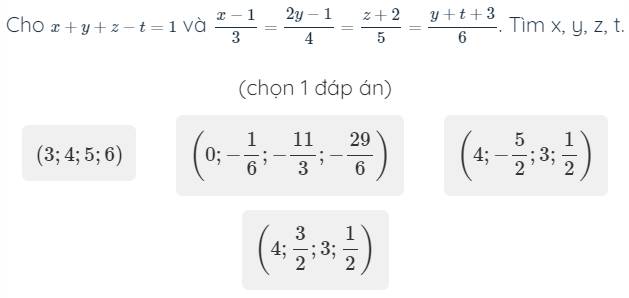
\(\dfrac{x-1}{3}=\dfrac{2y-1}{4}=\dfrac{z+2}{5}=\dfrac{y+t+3}{6}=\dfrac{\left(x-1\right)+\left(2y-1\right)+\left(z+2\right)-\left(y+t+3\right)}{3+4+5-6}\)
\(=\dfrac{x+y+z-t-3}{6}=\dfrac{1-3}{6}=-\dfrac{1}{3}\)
\(\Rightarrow\left\{{}\begin{matrix}\dfrac{x-1}{3}=-\dfrac{1}{3}\\\dfrac{2y-1}{4}=-\dfrac{1}{3}\\\dfrac{z+2}{5}=-\dfrac{1}{3}\\\dfrac{y+t+3}{6}=-\dfrac{1}{3}\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x=0\\y=-\dfrac{1}{6}\\z=-\dfrac{11}{3}\\t=-\dfrac{29}{6}\end{matrix}\right.\)
c.
\(\dfrac{x^2}{6}=\dfrac{24}{25}\)
\(\Rightarrow x^2=\dfrac{144}{25}=\left(\dfrac{12}{5}\right)^2\)
\(\Rightarrow x=\pm\dfrac{12}{5}\)