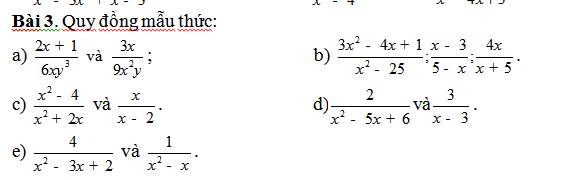Question

Answer 1

a.

$\frac{2x+1}{6xy^3}=\frac{2x+1}{6xy^3}$

$\frac{3x}{9x^2y}=\frac{1}{3xy}=\frac{2y^2}{6xy^3}$

b..

$\frac{3x^2-4x+1}{x^2-25}=\frac{3x^2-4x+1}{x^2-25}$

$\frac{x-3}{5-x}=\frac{3-x}{x-5}=\frac{(3-x)(x+5)}{(x-5)(x+5)}=\frac{-x^2-2x+15}{x^2-25}$

$\frac{4x}{x+5}=\frac{4x(x-5)}{(x-5)(x+5)}=\frac{4x^2-20x}{x^2-25}$

Answer 2

c.

$\frac{x^2-4}{x^2+2x}=\frac{(x-2)(x+2)}{x(x+2)}=\frac{x-2}{x}=\frac{(x-2)^2}{x(x-2)}$

$\frac{x}{x-2}=\frac{x^2}{x(x-2)}$

d.

$\frac{2}{x^2-5x+6}=\frac{2}{x^2-5x+6}$

$\frac{3}{x-3}=\frac{3(x-2)}{(x-2)(x-3)}=\frac{3x-6}{x^2-5x+6}$

e.

$\frac{4}{x^2-3x+2}=\frac{4}{(x-1)(x-2)}=\frac{4x}{x(x-1)(x-2)}$

$\frac{1}{x^2-x}=\frac{1}{x(x-1)}=\frac{x-2}{x(x-1)(x-2)}$