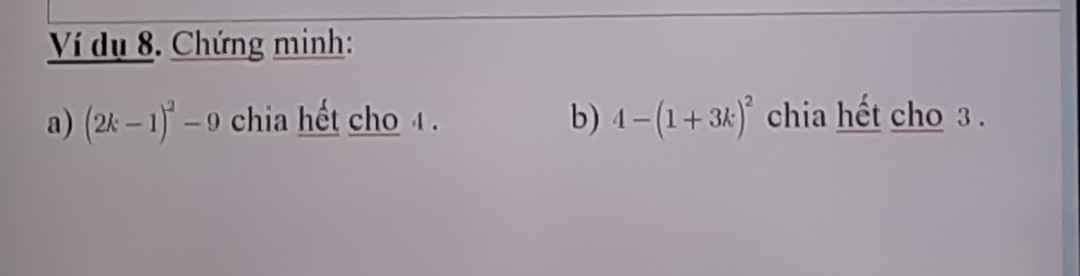Question

Answer 1

`a, (2k-1)^2-9 <=> (2k-1-3)(2k-1+3)`

`=(2k-4)(2k+2)=4(k-2)(k+1) vdots 4`.

`b, 4-(1+3k)^2=(2-1-3k)(2+1+3k)=(-1-3k)(3(1+k)) vdots 3.`

Answer 2

a)

`(2k-1)^2-9`

`=(2k-1-3)(2k-1+3)`

`=(2k-4)(2k+2)`

`=4(k-2)(k+1)`

có \(4⋮4=>4\left(k-2\right)\left(k+1\right)⋮4\) 

\(=>\left(2k-1\right)^2-9⋮4\)

b)

`4-(1+3k)^2`

`=(2-1-3k)(2+1+3k)`

`=(1-3k)(3+3k)`

`=3(1-3k)(1+k)`

có \(3⋮3=>3\left(1-3k\right)\left(1+k\right)⋮3\\ =>4-\left(1+3k\right)^2⋮3\)