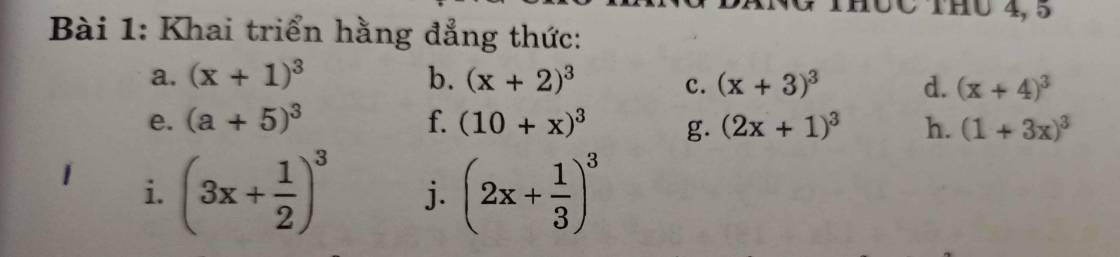a, `(x+1)^3 = x^3 + 3x^2 + 3x +1 `
b, `(x+2)^3 = x^3 + 6x^2 + 12x + 8 `
c, `(x+3)^3 = x^3 + 9x^2 + 27x + 27`
d, `(x+4)^3 = x^3 + 12x^2 + 48x + 64`
e, `(x+5)^3 = x^3 + 15x^2 + 75x + 25`
f, `( 10+x)^3 = 1000 + 300x + 30x^2 + x^3`
g,` ( 2x + 1)^3 = 8x^3 + 12x^2 + 6x + 1`
h,` (1 + 3x)^3 = 1+ 9x + 27x^2 + 9x^2`
i,` ( 3x + 1/2 )^3 = 27x^3 + 27x^2/2 + 9x/4 1/8`
j, `( 2x + 1/3)^3 = 8x^3 + 4x^2 + 2x/3 + 1/27`
Bài \(1\)
\(a)\)\(\left(x+1\right)^3=x^3+3.x^2.1+3.x.1^2+1^3=x^3+3x^2+3x+1\)
\(b)\)\(\left(x+2\right)^3=x^3+3.x^2.2+3.x.2^2+2^3=x^3+6x^2+12x+8\)
\(c)\)\(\left(x+3\right)^3=x^3+3.x^2.3+3.x.3^2+3^3=x^3+9x^2+27x+27\)
\(d)\)\(\left(x+4\right)^3=x^3+3.x^2.4+3.x.4^2+4^3=x^3+12x^2+48x+64\)
\(e)\)\(\left(a+5\right)^3=a^3+3.a^2.5+3.a.5^2+5^3=a^3+15a^2+75a+125\)
\(f)\)\(\left(10+x\right)^3\)
\(=10^3+3.10^2.x+3.10.x^2+x^3\)
\(=1000+300x+30x^2+x^3\)
\(=x^3+30x^2+300x+1000\)
\(g)\)\(\left(2x+1\right)^3\)
\(=\left[\left(2x\right)^3+3.\left(2x\right)^2.1+3.2x.1^2+1^3\right]\)
\(=8x^3+12x^2+6x+1\)
\(h)\)\(\left(1+3x\right)^3\)
\(=1^3+3.1^2.3x+3.1.\left(3x\right)^2+\left(3x\right)^3\)
\(=1+9x+27x^2+27x^3\)
\(=27x^3+27x^2+9x+1\)
\(i)\)\(\left(3x+\dfrac{1}{2}\right)^3\)
\(=\left(3x\right)^3+3.\left(3x\right)^2.\dfrac{1}{2}+3.3x.\left(\dfrac{1}{2}\right)^2+\left(\dfrac{1}{2}\right)^3\)
\(=27x^3+\dfrac{27}{2}x^2+\dfrac{9}{4}x+\dfrac{1}{8}\)
\(j)\)\(\left(2x+\dfrac{1}{3}\right)^3\)
\(=\left(2x\right)^3+3.\left(2x\right)^2.\dfrac{1}{3}+3.2x.\left(\dfrac{1}{3}\right)^2+ \left(\dfrac{1}{3}\right)^3\)
\(=8x^3+4x^2+\dfrac{2}{3}x+\dfrac{1}{27}\)