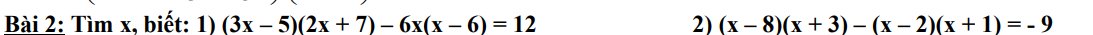`@` `\text {Ans}`
`\downarrow`
`1)`
`(3x - 5)(2x + 7) - 6x(x-6) = 12`
`<=> 3x(2x+7) - 5(2x + 7) - 6x^2 + 36x = 12`
`<=> 6x^2 + 21x - 10x - 35 - 6x^2 + 36x = 12`
`<=> (6x^2 - 6x^2) + (21x - 10x + 36x) - 35 = 12`
`<=> 47x - 35 = 12`
`<=> 47x = 12+35`
`<=> 47x = 47`
`<=> x = 1`
Vậy, `S = {1}`
`2)`
`(x - 8)(x + 3) - (x - 2)(x + 1) = -9`
`<=> x(x+3) - 8(x+3) - [ x(x+1) - 2(x+1)] = -9`
`<=> x^2 + 3x - 8x - 24 - (x^2 + x - 2x - 2) = -9`
`<=> x^2 + 3x - 8x - 24 - (x^2 - x - 2) = -9`
`<=> x^2 + 3x - 8x - 24 - x^2 + x + 2 = -9`
`<=> (x^2 - x^2) + (3x - 8x + x) + (-24 + 2) = -9`
`<=> -4x - 22 = -9`
`<=> -4x = 13`
`<=> x = -13/4`
Vậy, `S = {-13/4}.`
`@` `\text {Kaizuu lv uuu}`