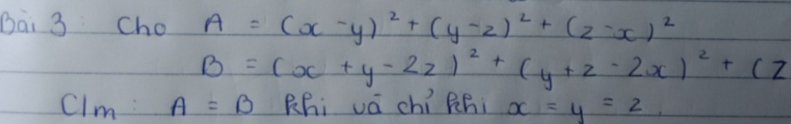Đặt \(a=x-y;b=y-z;c=z-x\) thì \(a+b+c=0\)
Khi đó:
\(A=a^2+b^2+c^2=0\)
\(B=\left(b-c\right)^2+\left(a-c\right)^2+\left(a-b\right)^2\)
Theo đề cho A = B ta có:
\(a^2+b^2+c^2=\left(a-b\right)^2+\left(b-c\right)^2+\left(a-c\right)^2\)
\(\Leftrightarrow-a^2-b^2-c^2+2ab+2bc+2ca=0\)
\(\Leftrightarrow a^2+b^2+c^2+2ab+2bc+2ca=2\left(a^2+b^2+c^2\right)\)
\(\Leftrightarrow2\left(a^2+b^2+c^2\right)=\left(a+b+c\right)^2=0\)
\(\Rightarrow a=b=c=0\)
\(\Rightarrow x=y=z\)
Vậy A = B khi và chỉ khi x = y = z
Đúng 3
Bình luận (0)
