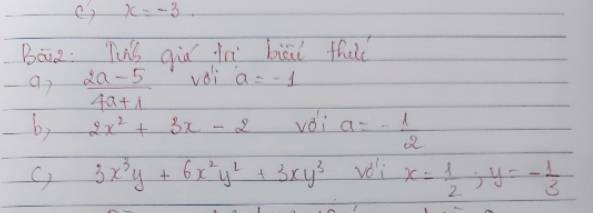\(a,\dfrac{2a-5}{4a+1}\)
Thay \(a=-1\) vào biểu thức trên \(\Rightarrow\dfrac{2.\left(-1\right)-5}{4.\left(-1\right)+1}=\dfrac{-2-5}{-4+1}=\dfrac{-7}{-3}=\dfrac{7}{3}\)
\(b,2x^2+3x-2\) ( Sửa : \(x=-\dfrac{1}{2}\) )
Thay \(x=-\dfrac{1}{2}\) vào biểu thức trên \(\Rightarrow2.\left(-\dfrac{1}{2}\right)^2+3.\left(-\dfrac{1}{2}\right)-2=\dfrac{1}{2}-\dfrac{3}{2}-2=-3\)
\(c,3x^3y+6x^2y^2+3xy^3\)
Thay \(x=\dfrac{1}{2};y=-\dfrac{1}{3}\) vào biểu thức trên \(\Rightarrow3.\left(\dfrac{1}{2}\right)^3.\left(-\dfrac{1}{3}\right)+6.\left(\dfrac{1}{2}\right)^2.\left(-\dfrac{1}{3}\right)^2+3.\dfrac{1}{2}.\left(-\dfrac{1}{3}\right)^3\)
\(=-\dfrac{1}{8}+\dfrac{1}{6}-\dfrac{1}{18}=-\dfrac{1}{72}\)
a)Thay \(a=-1\) vào biểu thức \(\dfrac{2a-5}{4a+1}\) ta được:\(\dfrac{2.\left(-1\right)-5}{4.\left(-1\right)+1}=\dfrac{-2-5}{-4+1}=\dfrac{-7}{-3}=\dfrac{7}{3}\)
b)Thay \(x=\dfrac{-1}{2}\) vào biểu thức \(2x^2+3x-2\) ta được:
\(2.\left(\dfrac{-1}{2}\right)^2+3.\dfrac{-1}{2}-2=2.\dfrac{1}{4}+\dfrac{-3}{2}-2=\dfrac{1}{2}-\dfrac{3}{2}-2=-3\)
c) Ta có:
\(3x^3y+6x^2y^2+3xy^3=3x\left(x^2y+2xy^2+y^3\right)\)
Thay \(x=\dfrac{1}{2};y=\dfrac{-1}{3}\) vào biểu thức \(3x\left(x^2y+2xy^2+y^3\right)\) ta được:
\(3.\dfrac{1}{2}\left[\left(\dfrac{1}{2}\right)^2.\dfrac{-1}{3}+2.\dfrac{1}{2}.\left(\dfrac{-1}{3}\right)^2+\left(\dfrac{-1}{3}\right)^3\right]\)
\(=\dfrac{3}{2}.\left(\dfrac{1}{4}.\dfrac{-1}{3}+1.\dfrac{1}{9}+\dfrac{-1}{27}\right)\)
\(=\dfrac{3}{2}.\left(\dfrac{-1}{12}+\dfrac{1}{9}-\dfrac{1}{27}\right)\)
\(=\dfrac{3}{2}.\dfrac{-1}{108}\)
\(=\dfrac{-1}{72}\)