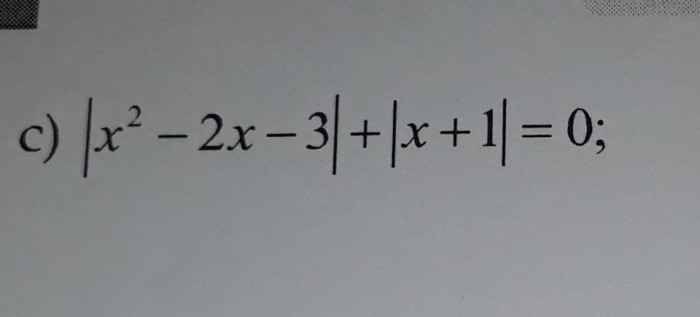`|x^2-2x-3|+|x+1|=0`
Vì `|x^2-2x-3|≥0 ∀x`
`|x+1|≥0 ∀x`
mà `|x^2-2x-3|+|x+1|=0`
`=>` \(\left\{{}\begin{matrix}\left|x^2-2x-3\right|=0\\\left|x+1\right|=0\end{matrix}\right.\)
`=>` \(\left\{{}\begin{matrix}x^2-3x+x-3=0\\x=-1\end{matrix}\right.\)
`=>` \(\left\{{}\begin{matrix}\left(x-3\right)\left(x+1\right)=0\\x=-1\end{matrix}\right.\)
`=>` \(\left\{{}\begin{matrix}\left[{}\begin{matrix}x=3\\x=-1\end{matrix}\right.\\x=-1\end{matrix}\right.\)
`=> x=-1`
Lời giải:
Ta có:
$|x^2-2x-3|\geq 0; |x+1|\geq 0$ với mọi $x$
Do đó để tổng của chúng bằng $0$ thì:
$x^2-2x-3=x+1=0$
$\Leftrightarrow (x+1)(x-3)=x+1=0$
$\Leftrightarrow x+1=0$
$\Leftrightarrow x=-1$