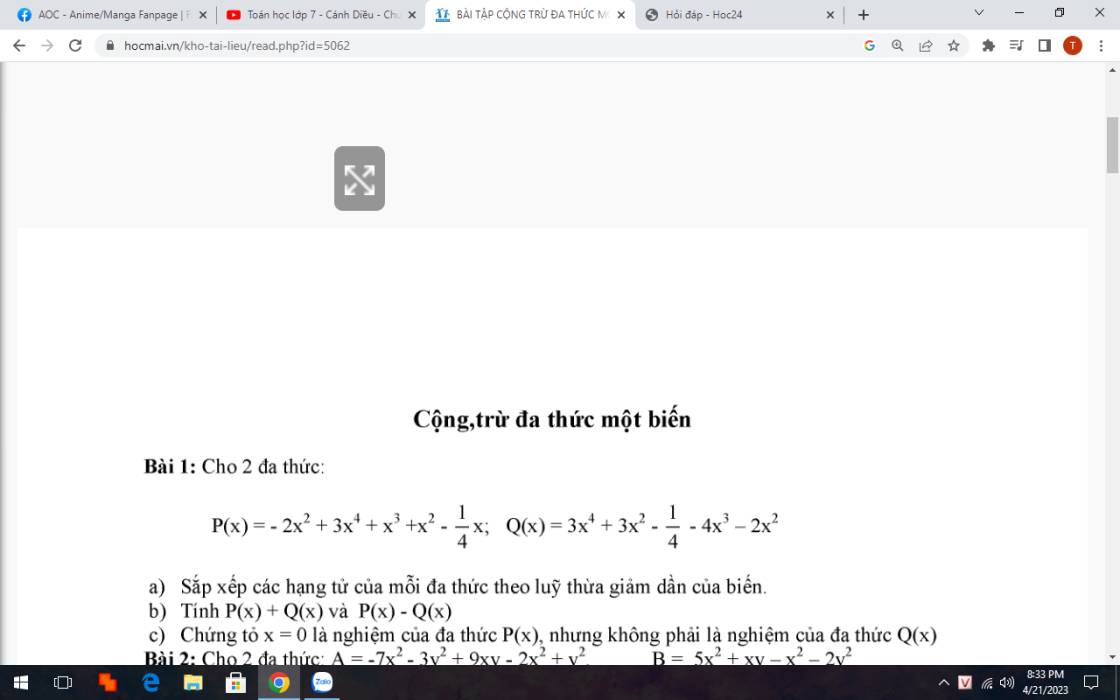
a.
\(P\left(x\right)=3x^4+x^3-x^2-\dfrac{1}{4}x\)
\(Q\left(x\right)=3x^4-4x^3+x^2-\dfrac{1}{4}\)
b.
\(P\left(x\right)+Q\left(x\right)=6x^4-3x^3-\dfrac{1}{4}x-\dfrac{1}{4}\)
\(P\left(x\right)-Q\left(x\right)=5x^3-2x^2-\dfrac{1}{4}x+\dfrac{1}{4}\)
c.
Thay \(x=0\) vào \(P\left(x\right)\) ta được:
\(P\left(0\right)=3.0^4+0^3-0^2-\dfrac{1}{4}.0=0\)
\(\Rightarrow x=0\) là nghiệm của đa thức \(P\left(x\right)\)
Thay \(x=0\) vào \(Q\left(x\right)\) ta được
\(Q\left(0\right)=3.0^4-4.0^3+0^2-\dfrac{1}{4}=-\dfrac{1}{4}\ne0\)
\(\Rightarrow x=0\) không phải là nghiệm của Q(x)
Vậy \(x=0\) là nghiệm của \(P\left(x\right)\) nhưng không là nghiệm của \(Q\left(x\right)\)